Urednik strani: Klavdija Slapar, za vsa vprašanja se obrnite na e-naslov: klavdija.slapar@os-trebnje.si
REŠITVE ANKETE
Naloge in rešitve v word dokumentu lahko najdete tukaj, kjer si jih lahko natisnete in prilepite v zvezek. Sicer pa si rešitve prepišite v zvezek.
10. TEDEN
od 25. 5. do 29. 5. 2020
1.URA: Ponedeljek 25. 5. 2020
UTRJEVANJE:
Klikni na dano povezavo https://www.1ka.si/a/285608 in reši anketo.
OBSEG IN PLOŠČINA TRAPEZA
Oglej posnetek video predstavitev, ki sem ga pripravila za vas. V zvezek si prepiši vsebino, ki je v video predstavitvi ali v zapiskih, ki sledijo.
PONOVITEV SNOVI:
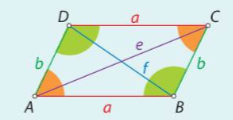
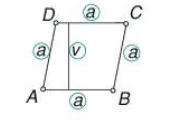
TRAPEZ:
Je štirikotnik, ki ima en par vzporednih stranic: a in c, ki jih imenujemo osnovnici, nevzporedni stranici b in d sta kraka. Pravokotna razdalja med nosilkama osnovnic je višina trapeza (ima samo eno višino, saj ima samo en par vzporednih stranic).
ENAKOKRAKI TRAPEZ:
Je trapez, ki ima oba kraka skladna (b=d).
NOVA SNOV:
OBSEG TRAPEZA: o = a + b + c + d
OBSEG ENAKOKRAKEGA TRAPEZA:
o = a + b + c + b
o = a + 2 × b + c
s … srednjica trapeza
s=(a+c)/2
PLOŠČINA TRAPEZA:
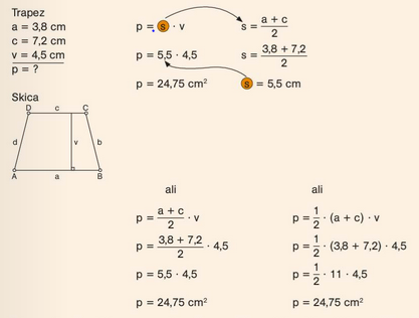
p = s ⋅ v
p=(a+c )/2 × v ali p=1/2 × (a + c) × v
PRIMERI:
1. Primer:
2. Primer:
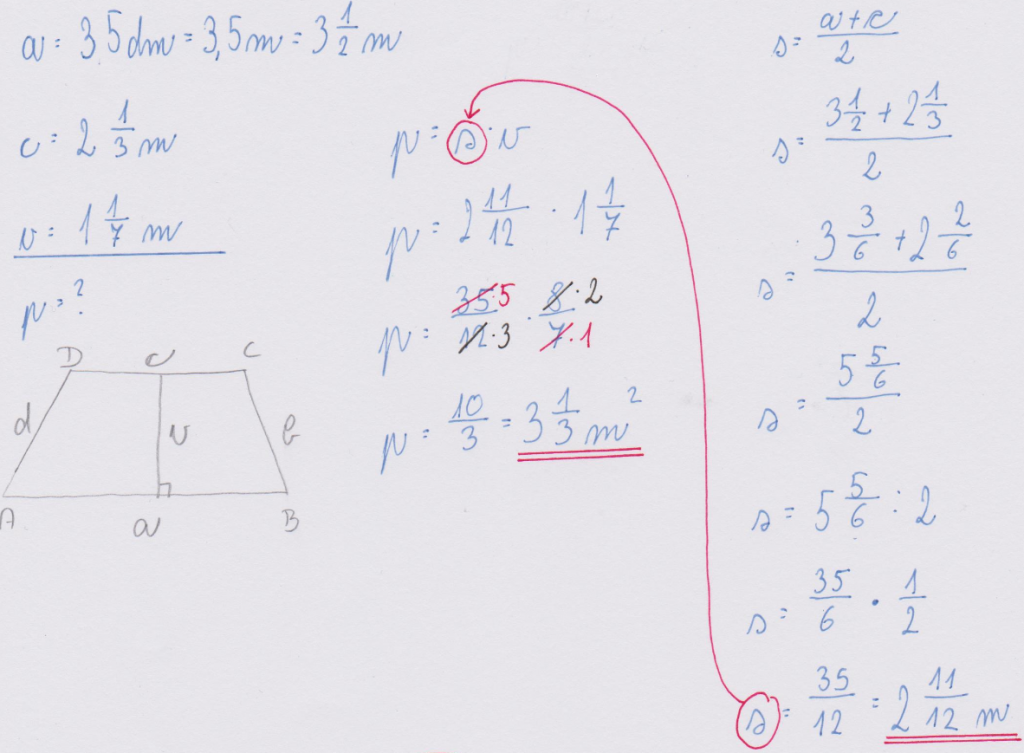
3. Primer:
NALOGE:
V DZ 5, na straneh od 28 do 31 reši vsaj naslednje naloge 4. b, c, 5. b, c, 6. a ter preveri rešitve.
2.URA: Sreda 27. 5. 2020
OBSEG IN PLOŠČINA LIKOV S PRAVOKOTNIMA
DIAGONALAMA (ROMB, KVADRAT IN DELTOID)
Oglej posnetek video predstavitev, ki sem ga pripravila za vas. V zvezek si prepiši vsebino, ki je v video predstavitvi ali v zapiskih, ki sledijo.
OBSEG DELTOIDA: o = a + a + c + c
o = 2 × a + 2 × c
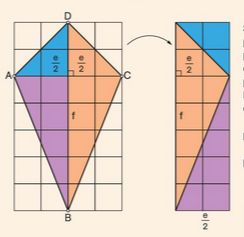
PLOŠČINA DELTOIDA:
p = e/2 × f=(e × f)/2= 1/2 × e × f
Ploščina štirikotnika s pravokotnima diagonalama (romb, deltoid in kvadrat) je enaka polovici produkta obeh diagonal.
PRIMERI:
1. Primer:
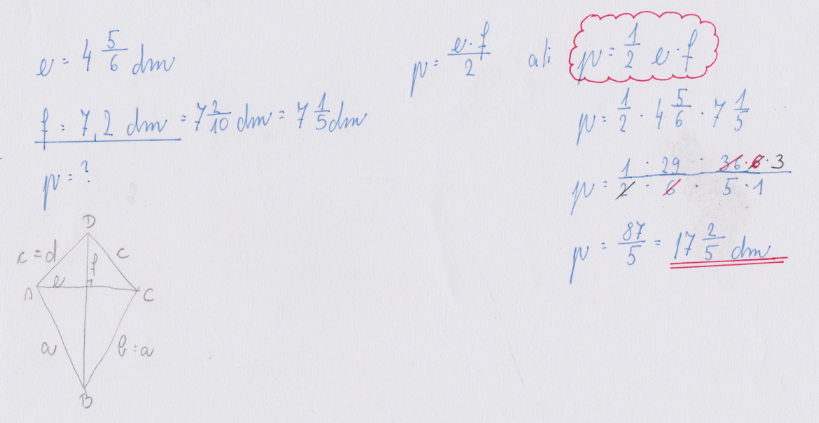
2. Primer:
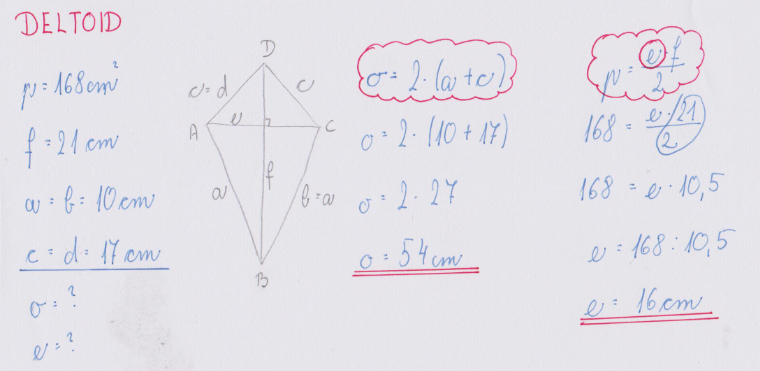
3. Primer: DZ 5, str. 38, 4. naloga

4. Primer: DZ 5, str. 38, 4. naloga
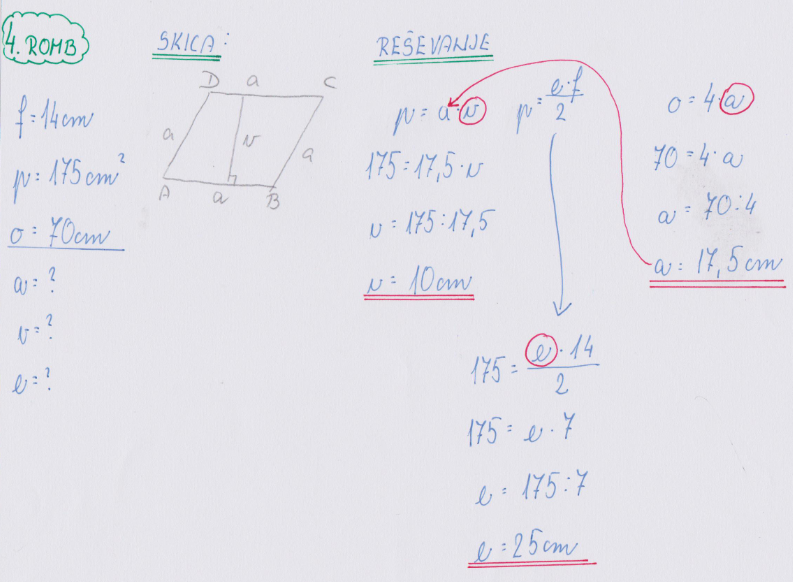
NALOGE:
V DZ 5, na straneh od 34 do 39 reši vsaj naslednje naloge 2. b, c, 3. b, 4. (1. romb) ter preveri rešitve.
DODATNE NALOGE: 3 b, 4 (1., 3. romb)
_________________________________________________________________________________________
NOVO: Ocene pisnega preizkusa.
REŠITVE OCENJEVANJA ZNANJA
ODSTOTKI, TRIKOTNIKI IN ŠTIRIKOTNIKI
PISNO OCENJEVANJE ZNANJA IZ MATEMATIKE
Naloge in rešitve v word dokumentu lahko najdete tukaj , kjer si jih lahko natisnete in prilepite v zvezek.
1. NALOGA: Izpolni tabelo. Pri zapisu okrajšanega ulomka, ulomkovo črto nadomesti s poševnico (/). _____/ 6 T
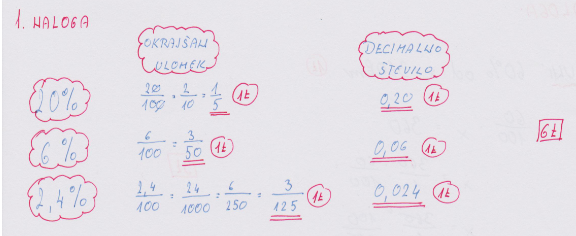
2. NALOGA: Izračunaj. Ne pozabi zapisati enote, kjer je to potrebno. _____/ 4 T

3. NALOGA: Trener je kolesarjem povedal, da so prevozili 360 km, kar je 60% načrtovane poti. Koliko km meri ceotno pot? _______ / 3 T
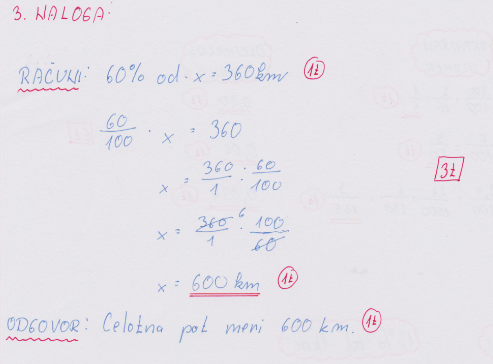
4. NALOGA: Anže porabi za pot do šole 45 minut. 36 minut se vozi z avtobusom. Koliko odstokov časa hodi peš? _____/ 1T
20%
45%
80%

5.* NALOGA: Miza je stala 800 €. Ceno so zvišali za 10 %, nato pa znižali za 20 %. Koliko stane miza sedaj? _____/ 4 T

6. NALOGA: Označi ali je izjava pravilna (P) ali nepravilna (N). ______ / 5T
| Vpiši besedilo | |
| V enakokrakem trikotniku sta dva kota skladna. | P |
| V enakostraničnem trikotniku je vsota zunanjih kotov 180°. | N |
| Trikotnik, ki ima en pravi kot, imenujemo topokotni trikotnik. | N |
| Paralelogram je osno someren lik. | N |
| Pri rombu sta nasprotna kota skladna. | P |
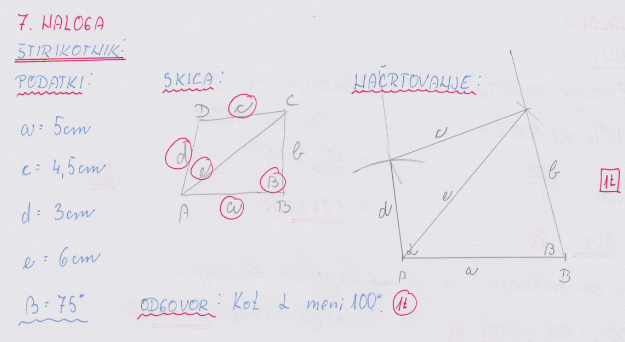
7. NALOGA: Načrtaj štirikotnik ABCD s podatki a = 5 cm, c = 4,5 cm, d = 3 cm, e = 6 cm in β = 75°. Kot α meri _____ / 1T
80
100°
120°
8. NALOGA: Nariši enakokraki trapez ABCD s podatki c = 3,5 cm, v = 3 cm in δ = 110°. Koliko je dolga stranica a? Obvezna skica. ______ / 4 T
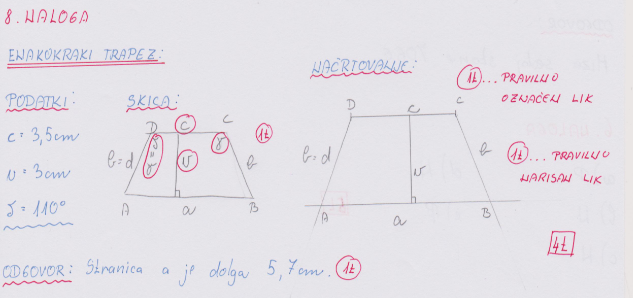
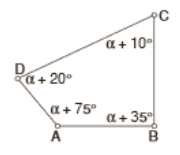
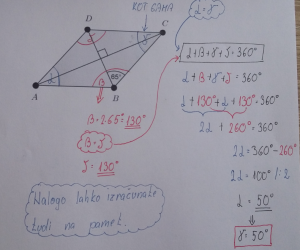
9. DODATNA NALOGA: Izračunaj neznani kot α. ______/ 3T
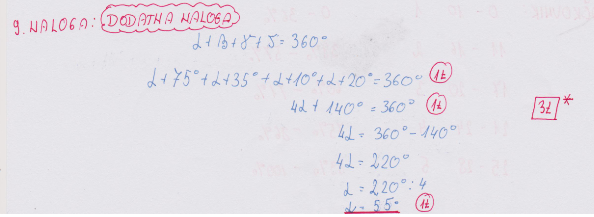
9. TEDEN
od 18. 5. do 22. 5. 2020
OCENJEVANJE ZNANJA:
V sredo, 20. 5. 2020, bomo od 11.00 do 12.00 preko sistema 1ka pisali pisni preizkus – anketo iz matematike.
POVEZAVE DO OCENJEVANJA BOSTE NAŠLI TUKAJ:
Povezava do ocenjevanja znanja: https://www.1ka.si/a/283271
Povezava do ocenjevanja znanja za učence, ki imajo DSP: https://www.1ka.si/a/283937
NAVODILA ZA PISNO OCENJEVANJE ZNANJA:
Pred ocenjevanjem znanja pa še enkrat natančno preberi navodila:
– V tej anketi boš preveril svoje znanje o ODSTOTKIH, TRIKOTNIKIH, ŠTIRIKOTNIKIH.
– Na razpolago boste imeli 60 minut, učenci, ki imate DSP pa 75 minut.
– Nekaj nalog bo potrebno tudi slikati in oddati kot priponko k anketi.
– Pisni preizkus je obvezen za vse, ki v 2. ocenjevalnem obdobju še nimate ocene. Tisti, ki ste oceno pridobili s popravljanjem negativne ocene, ne nadomesti ocene v 2. oc. obdobju.
– Ostali učenci boste imeli na anketi vprašanje ali želite, da sem vam anketa oceni ali ne. Če bo odgovor da, se anketa oceni, sicer ne. Ocena, ki jo boste pridobili, bo bolj informativne narave. Zaključevalo se bo pretežno na podlagi preteklih ocen.
– Učenci, ki ste bili do 16. marca med oceno, pa bo ta ocena lahko vplivala na zaključevanje (navzgor/navzdol).
– Če se kdo skupnega ocenjevanja ne bo udeležil, pa nujno potrebuje oceno, bo pozvan k ocenjevanju preko aplikacije Zoom, po 25. maju bo lahko vprašan tudi v šoli. Enako velja, če bo pisal negativno.
– Verjamem, da boste reševali pošteno in pokazali svoje realno znanje. Če pa bom vseeno sumila na goljufijo, bom pozvala vse učence, ki bi bili lahko vpleteni, k zagovoru – SE NE SPLAČA!
VAJE ZA PISNO OCENJEVANJE ZNANJA:
Nekateri učenci ste mi pisali, da želite več vaj za pripravo na ocenjevanje znanja. Za vas sem pripravila učni list z rešitvami. Klikni na spodnjo povezavo:
Vaje za ocenjevanje znanja_TRIKOTNIKI, ŠTIRIKOTNIKI, ODSTOTKI
Vaje so namenjene učencem, ki bi radi še bolj utrdili snov. Vaje niso obvezne.
1. URA: 18. 5. 2020
OBSEG IN PLOŠČINA PARALELOGRAMA
V zvezek prepiši besedilo, ki ni zapisano poševno.
PONOVIMO:
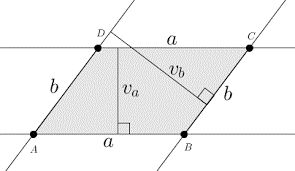
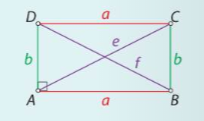
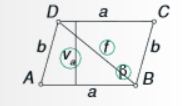
Paralelogram je štirikotnik, ki ima dva para vzporednih in skladnih stranic (a=c, b=d). Višina 𝑣𝑎 𝑖𝑛 𝑣𝑏 sta pravokotni razdalji med vzporednima stranicama.
NOVA SNOV:
Na povezavi https://www.youtube.com/watch?v=_XYEaglmoJs si oglej posnetek. Nato si v zvezek zapiši vso razlago, ki je na posnetku ali zapisana pod povezavo.
Video posnetki, kjer je razlaga reševaja vaj, sledijo v nadaljevanju.
OBSEG PARALELOGRAMA:
Obseg je seštevek dolžin vseh stranic paralelograma. Ker ima paralelogram po dve in dve stranici enako dolgi, se obseg izračuna po enačbi:
𝒐 = 𝟐 ∙ 𝒂 + 𝟐 ∙ 𝒃
PLOŠČINA PARALELOGRAMA:
Paralelogram preoblikujemo v pravokotnik, ki mu znamo izračunati ploščino. Slika prikazuje, kako smo del paralelograma odrezali. Odrezani del smo na desni strani lika dopolnili v pravokotnik.
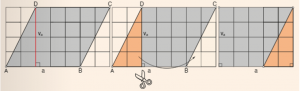
Paralelogram smo preoblikovali v ploščinsko enak pravokotnik z dolžino, ki je enaka stranici a, in širino, ki je enaka višini paralelograma va. Lahko ga preoblikujemo tudi v pravokotnik z dolžino b in širino vb.
Ploščina preoblikovanega pravokotnika je produkt dolžine in širine, torej se ploščina paralograma izračuna po formuli:
𝒑 = 𝒂 ∙ 𝒗𝒂 ali 𝒑 = 𝒃 ∙ 𝒗𝒃
Katero formulo uporabiti? Odvisno od podanih podatkov, ali imamo podano va ali vb.
PRIMERI:
1. PRIMER:
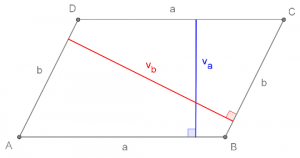
Izračunaj neznane količine paralelograma. To je direktna naloga, kjer le vstavimo podatke v enačbo, zato nalogo najprej rešite sami, nato preverite rešitve.
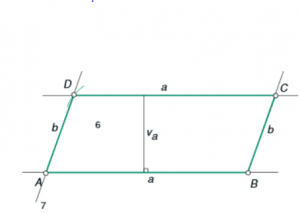
𝑎 = 6 𝑐𝑚
𝑣𝑎 = 6 cm
𝑏 = 7 𝑐𝑚
𝑜 =?
𝑝 =?
SKICA:
REŠEVANJE:
𝑜 = 2 ∙ 𝑎 + 2 ∙ 𝑏
𝑜 = 2 ∙ 6 + 2 ∙ 7
𝑜 = 12 + 14
𝑜 = 26 𝑐𝑚
Kako ugotoviti katero formulo uporabiti za računanje ploščine?
Odvisno od podanih podatkov, ali imamo podano va ali vb. Za računanje ploščine imamo podano va, torej bomo uporabili stranico a in uporabili enačbo:
𝑝 = 𝑎 ∙𝑣𝑎
𝑝 = 6 ∙ 6
𝑝 = 36 𝑐𝑚2
2. PRIMER: Na povezavi https://www.youtube.com/watch?v=57JMvG-lGrY si oglej posnetek razlage reševanja primera. Nato si v zvezek zapiši vso razlago, ki je na posnetku ali zapisana spodaj,
Ulomki so zapisani s poševnico, v zvezek jih pišite tako, kot smo jih pisali v šoli.
𝑎 = 3/4 d𝑚 =75/100 dm = 0,75 dm =7,5 cm
𝑣𝑎 = 0,12 d𝑚 = 1,2 cm
v𝑏 = 5 𝑐𝑚______________
o =?
p =?
SKICA:

REŠEVANJE:
1. p = a × va
p = 7,5 × 1,2
p = 9 cm2
2. p = b × vb
9 = b × 5
b = 9 : 5
b = 1,8 cm
3. 𝑜 = 2 ∙ 𝑎 + 2 ∙ 𝑏
𝑜 = 2 ∙ 7,5 + 2 ∙ 1,8
𝑜 = 15 + 3,6
𝑜 = 18, 6 𝑐𝑚
3. PRIMER: DZ 5, str. 23, naloga: 10. č
Na povezavi https://www.youtube.com/watch?v=iCSl3MM6SUM&t=5s si oglej posnetek video predstavitve. Nato si v zvezek zapiši vso razlago, ki je na posnetku ali pa je zapisana spodaj.
b = 4 cm
vb = 6,3 cm
o = 39 cm
a =?
p =?
SKICA:

REŠEVANJE:
1. p = b × vb
p = 4 × 6,3
p = 25,2 cm2
2. 𝑜 = 2 ∙ 𝑎 + 2 ∙ 𝑏
39 = 2 ∙ 𝑎 + 2 ∙ 4
39 = 2 ∙ 𝑎 + 8
2 ∙ 𝑎 = 39 – 8
2 ∙ 𝑎 = 31
a = 31 : 2
a = 15,5 cm
NALOGE: V DZ, 5 del, od 20 do 25 strani reši vsaj naslednje naloge 1 b, c, 4 b, č, 5 a, c*, 9 in preveri rešitve.
DODATNE NALOGE: Tisti, ki zmorete, lahko rešite še naloge: 6. in 8. b.
2. URA: 22. 5. 2020
OBSEG IN PLOŠČINA ROMBA
PONOVIMO:
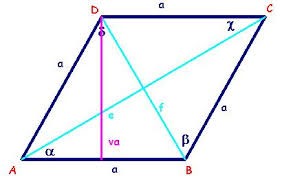
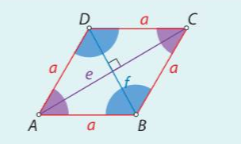
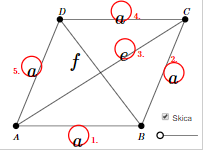
Romb je štirikotnik, ki ima dva para vzporednih in skladnih stranic (a=b=c=d). Višina v je pravokotna razdalji med vzporednima stranicama. Diagonali e in f se pravokotno razpolavljata.
NOVA SNOV:
Na povezavi https://www.youtube.com/watch?v=3eoJpCusEmE si oglej posnetek video predstavitve. Nato si v zvezek zapiši vso razlago, ki je na posnetku.
OBSEG:
Obseg je seštevek dolžin vseh stranic romba. Ker ima romb vse štiri stranice enako dolge, se obseg izračuna: 𝒐 = 𝟒 ∙ 𝒂
PLOŠČINA:
Romb (tako kot paralelogram) preoblikujemo v pravokotnik, ki mu znamo izračunati ploščino. Slika prikazuje, kako smo del romba odrezali (rumeno). Odrezani del smo na desni strani lika dopolnili v pravokotnik.
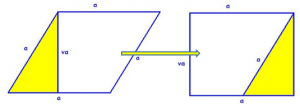
Romb smo preoblikovali v ploščinsko enak pravokotnik z dolžino, ki je enaka stranici a, in širino, ki je enaka višini v. Ploščina preoblikovanega pravokotnika je produkt dolžine in širine, torej se ploščina romba izračuna po formuli: 𝒑 = 𝒂 ∙ va
PRIMERI:
1. PRIMER: Na povezavi https://www.youtube.com/watch?v=NEjXbcjOAQk si oglej posnetek razlage reševanja primera. Nato si v zvezek zapiši vso razlago, ki je na posnetku ali zapisana spodaj.
𝑎 = 16 𝑐𝑚
𝑣 =va = 3,2 dm = 32 𝑐𝑚
o = ?
p = ?
SKICA:
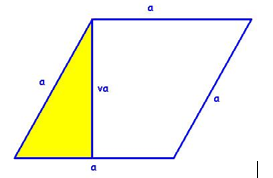
REŠEVANJE:
o = 4 × a
o = 4 × 16
o = 64 cm
p = a × va
p = 16 × 32
p = 512 cm2
2. PRIMER: DZ , 5. del, stran 25, 10. naloga (2. primer)
Na povezavi https://www.youtube.com/watch?v=Jwe5-QMW7rk si oglej posnetek razlage reševanja primera. Nato si v zvezek zapiši vso razlago, ki je na posnetku ali zapisana spodaj.
v = 1 1/3 d𝑚
o = 4 2/3 dm
a = ?
p = ?
SKICA:

REŠEVANJE:
o = 4 × a
4 2/3 = 4 × a
a = 4 2/3: 4
a = 14/3 : 4/1
a = 14/3 × ¼
a = 7/6
a = 1 1/6 dm
p = a × va
p = 1 1/6 × 1 1/3
p = 7/6 × 4/3
p = 14/9
p = 1 5/9 dm2
NALOGE:
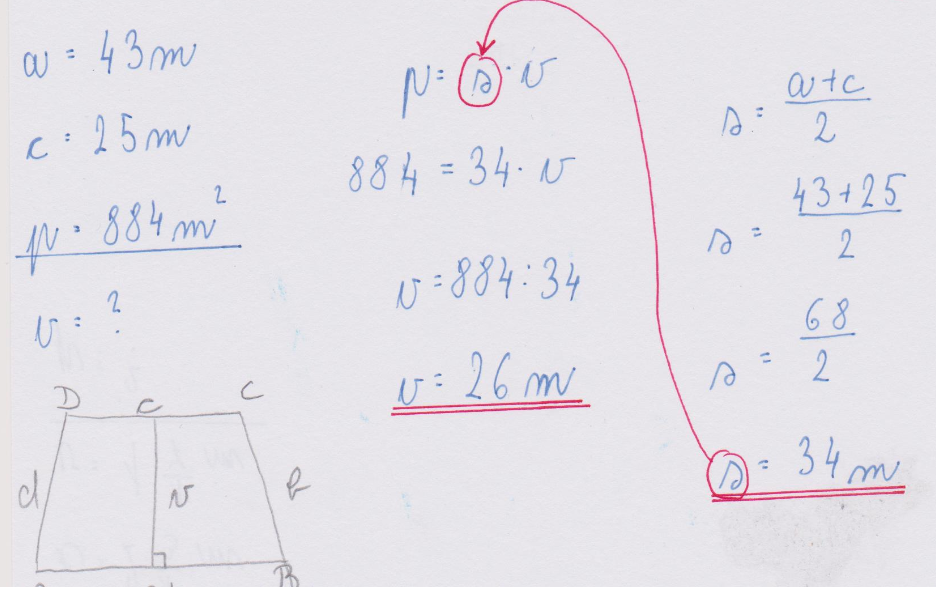
V DZ, 5 del, na strani 24 in 25 reši naloge: 7, 10 (1.primer in 3*primer – boljši učenci. Ostali rešite primer, ki je tudi v navodilih posnetka (2. primer): o= 60 m, p = 72m2, a = ?, v = ? ) in preveri rešitve (rešitev dodanega primera: a = 15 cm, v = 4, 8 cm).
________________________________________________________________________________________
8. TEDEN
od 11. 5. do 15. 5. 2020
POMEMBNO!
NAVODILA ZA PISNI PREIZKUS ZNANJA:
- V sredo, 20. 5. 2020, bomo od 11.00 do 12.00 preko sistema 1ka pisali pisni preizkus – anketo iz matematike, tokrat za oceno.
- Povezava do ankete bo na spletni strani že kakšnem dan prej, aktivna pa bo ob uri pisanja.
- Pisni preizkus je obvezen za vse učence, ki v 2. ocenjevalnem obdobju še nimajo ocene.
- Ostali učenci boste imeli na anketi vprašanje ali želite, da sem vam anketa oceni ali ne. Če bo odgovor da, se anketa oceni, sicer ne.
- Ocena, ki jo boste pridobili, bo bolj informativne narave, zaključevalo se bo pretežno na podlagi preteklih ocen. Učenci, ki ste bili do 16. marca med oceno, pa bo ta ocena lahko vplivala na zaključevanje (navzgor/navzdol).
- Vsi boste imeli zaradi izrednih razmer podaljšan čas pisanja, 60 minut.
- Če se kdo skupnega ocenjevanja ne bo udeležil,pa nujno potrebuje oceno, bo pozvan k ocenjevanju preko aplikacije Zoom. Enako velja, če bo pisal negativno, učitelj podvomi o verodostojnosti ankete (možnost goljufije) oziroma, učitelju pri popravljanju kaj ne bo jasno. V primeru, da se vrnemo v šolo, bo lahko opravil razgovor tudi v šoli.
- Pri pisanju imejte pripravljen tudi fotoaparat ali mobilni telefon, da boste lahko poslali sliko vašega izdelka, v kolikor bo anketa to zahtevala (podobno, kot ste že pripenjali slike do sedaj). Pripravljene imejte tudi ustrezne pripomočke za načrtovaje likov (geotrikotnik, šestilo, ošiljen svinčnik).
- Vsebine, ki se bodo preverjale, si oglejte v navodilih preteklega tedna.
1.URA: Ponedeljek 11. 5. 2020
OBSEG IN PLOŠČINA LIKOV
Ta teden ni ankete. Pripravljajte se na ocenjevanje znanja.
Oglej posnetek video predstavitev, ki sem ga pripravila za vas. V zvezek si prepiši vsebino, ki je v video predstavitvi ali v zapiskih, ki sledijo.
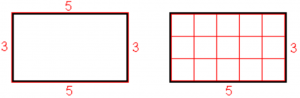
OBSEG LIKA je vsota dolžin vseh njegovih stranic.
Obseg lika merimo v m, dm, cm, mm.
o = 5 + 3 + 5 + 3 = 16
PLOŠČINA LIKA je število, ki nam pove, koliko ploščinskih enot (enotskih kvadratkov) potrebujemo, da dani lik popolnoma prekrijemo. Merimo jo v kvadratnih enotah (npr. m2, dm2, cm2, mm2)
p = 5 × 3 = 15 e2
PRIMERI:
1. PRIMER: Izračunaj obseg in ploščino večkotnika.
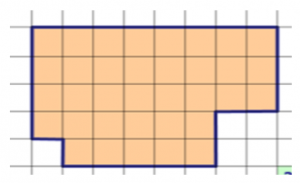
Obseg lika: o = 26 cm
Ploščina lika: p = 35 cm2
2. PRIMER:
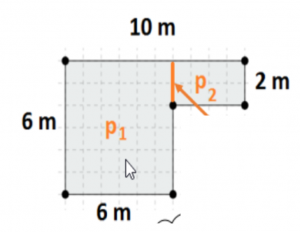
Obseg lika: o = 6 m + 6 m + 4 m + 4 m + 2 m + 10 m = 32 m
Ploščina lika:
p1= 6 × 6 = 36 m2
p2= 2 × 4 = 8 m2
p = p1+ p2 = 8 + 36 = 44 m2
3. PRIMER:
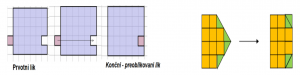
Ugotovitev:
- Ker je nov lik sestavljen iz enakih delov kot prvotni lik, sta njuni ploščini enaki.
- S preštevanjem stranic kvadratkov, ki lik omejujejo, ugotovimo, da obsega nista enaka.
NALOGE:
V DZ 7, 5. del, na straneh od 7 do 10 reši vsaj naslednje naloge 1, 3, 4, 6, 7*, 8, 9 a, d ter preveri rešitve.
Tisti, ki zmorete več, lahko rešite še ostale naloge.
2. URA: Sreda 13. 5. 2020
OBSEG IN PLOŠČINA PRAVOKOTNIKA IN KVADRATA
Oglej posnetek video predstavitev, ki sem ga pripravila za vas. V zvezek si prepiši vsebino, ki je v video predstavitvi ali v zapiskih, ki sledijo.
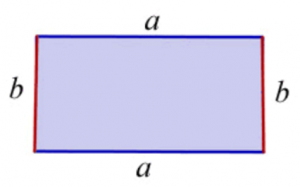
Obseg pravokotnika je vsota dolžin stranic pravokotnika.
o = a + b + a + b
o = 2 ⋅ a + 2 ⋅ b
o = 2 ⋅ (a + b)
Ploščina pravokotnika je enaka zmnožku dolžine in širine pravokotnika
p = a ⋅ b
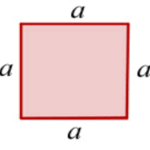
Obseg kvadrata je enak štirikratniku njegove dolžine.
o = a + a + a + a
o = 4 ⋅ a
Ploščina kvadrata je zmnožek dolžine in širine kvadrata.
Ker je dolžina enaka širini, je ploščina kvadrata
s stranico a enaka a2.
p = a ⋅ a
p = a2
PRIMERI:
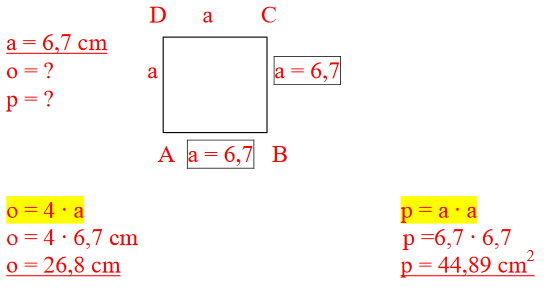
1. PRIMER: Izračunaj obseg in ploščino kvadrata z danimi podatki.
2. PRIMER: Izračunaj obseg in ploščino kvadrata z danimi podatki.
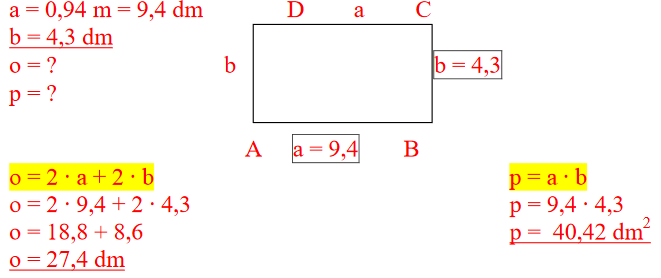
3. PRIMER: Izračunaj obseg in ploščino kvadrata, če poznaš obseg kvadrata.
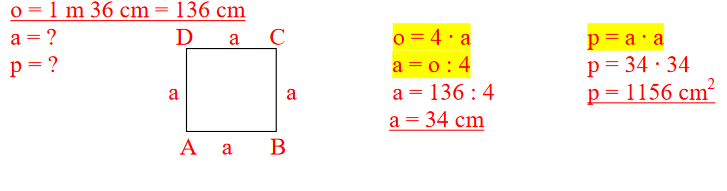
4. PRIMER: Izračunaj manjkajočo stranico in ploščino pravokotnika, če poznaš obseg in dolžino stranice.
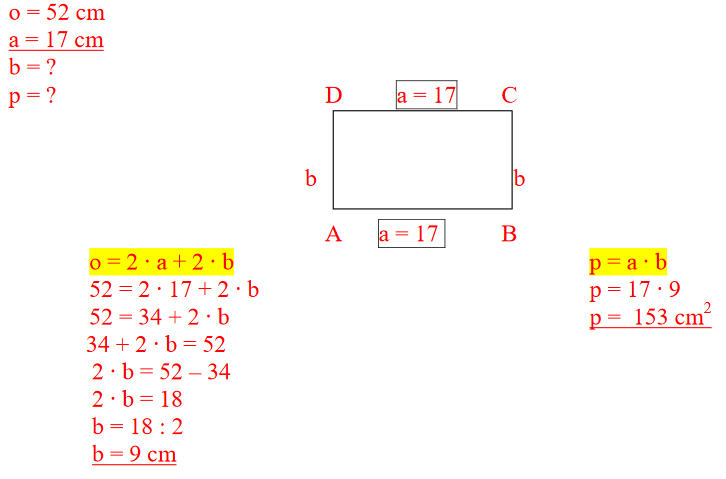
NALOGE:
V DZ 5, na straneh od 13 do 17 reši vsaj naslednje naloge: 1 b, 2. a, 4, 5. a, 6, 8, 9 ter preveri rešitve.
DODATNE NALOGE: Tisti, ki zmorete več, lahko rešite še naloge: 7, 10, 14
________________________________________________________________________________________
POPRAVI NAPAKO: V tabeli (lastnosti štirikotnikov), popravite nastalo napako: pri diagonalah pravokotnika, se diagonali ne sekata pod pravim kotom.
Se opravičujem za nastalo napako.
ANALIZA PREVERJANJA ZNANJA
Pet učencev je v anketi izpolnilo le začetni del, niste pa rešili nobene matematične naloge, zato vam tega ne bom upoštevala kot opravljeno nalogo.
- Anketo je rešilo 83 od 95 učencev, to je 87,40 % vseh učencev.
- 56% učencev je odgovorilo, da snov dobro razume, 44 % delno.
- 79% učencev je rešilo vse naloge, ter 21% učencev je naloge rešilo delno.
- 95% učencem video predavanje pomaga pri razumevanju snovi, 5% pa ne.
- Delež rešitev po nalogah:
- 1. nalogo je pravilno rešilo približno 53% vseh učencev.
- 2. nalogo je pravilno rešilo 94% vseh učencev.
- 3. nalogo je pravilno rešilo 85% vseh učencev.
- 4. nalogo je pravilno rešilo 69% vseh učencev.
- 6. nalogo je pravilno rešilo približno 32%vseh učencev.
- 7. nalogo je pravilno rešilo približno 43% vseh učencev.
- 8. nalogo je pravilno rešilo približno 66% vseh učencev.
- 9. nalogo je pravilno rešilo 47% vseh učencev.
- 10. nalogo je pravilno rešilo približno 56 % vseh učencev.
- 18% učencev meni, da so naloge pretežke, 82% učencev meni, da so naloge ravno prav težke in 0% učencev meni, da so naloge prelahke.
- Odgovori na nekatera vaša vprašanja oz trditve:
- Malo manj nalog pri anketah.
V tem tednu je bilo res malce več nalog v preverjanju kot običajno. Naloge so bile namenjene predvsem utrjevanju in pripravi na ocenjevanje znanje. Snov je bila obsežna, zato je bilo tudi težko izbrati le nekaj nalog, s katerimi bi preverili celotno snov. V naslednjih preverjanih vam obljubim, da bo zopet manj nalog, saj bomo preverjali le snov enega tedna nazaj. Naj pa vas razveselim z eno spodbudno novico, za prihodnji teden ne bo preverjanja.
- Mi še nismo obravnavalli zaporedij in vzorcev.
Res je, nekatere skupine še niso obravnavale zaporedij in vzorcev, zato je bil v preverjanju tudi enostavnejši primer. Podobne primere ste sicer že reševali v nižjih razredih. Predvidevala sem, da večjih težav tudi ostali ne bodo imeli. Moja predvidevanja so potrdili tudi dobri rezultati. V ocenjevanju pa se bom takšnih nalog izognila.
- Odstotke sem malo pozabila, zato mi ne gredo najbolje.
Res je že kar nekaj časa od spoznavanja odstotkov. Priporčam vam, da ponovno rešite kakšno izmed nalog iz delovnega zvezka ali zvezka in snov ponovite. Vrjamem, da se boste hitro spomnili poteka reševanja. Če pa še vedno ne bo šlo ali boste imeli vprašanje, mi pišite, vam bom pomagala.
- Veliko je likov in jih hitro lahko pomešaš.
Spoznali smo veliko različnih likov. Vsak pa ima tudi kar nekaj lastnosti, ki so zelo pomembne, predvsem pri načrtovanju, kasneje tudi pri računanju ploščin in obsegov. Zato vas tudi večkrat opomnim, da je pomembna skica, s pomočjo katere lahko naštejete lastnosti danega lika. Za začetek naj vam bo v pomoč tabela, ki sem vam jo sestavila.
- Razlaga v video predvajanju mi je zelo všeč,video posnetek mi je pomagal pri razumevanju snovi, odlično izdelana tabela,…
Hvala za vse pohvale in spodbudne besede. Me veseli, da vam je razlaga in tabela všeč in vam to omogoča lažje in hitrejše razumevanje snovi.
REŠITVE PREVERJANJA ZNANJA PRED OCENEJVANJEM
Naloge in rešitve v word dokumentu lahko najdete tukaj, kjer si jih lahko natisnete in prilepite v zvezek. Sicer pa si rešitve prepišite v zvezek.
1. NALOGA: Izpolni tabelo.Pri zapisu okrajšanega ulomka, ulomkovo črto nadomesti s poševnico (/).
| okrajšan ulomek | decimalno število | odstotki | |
| 5/100 | 1/20 | 0,05 | 5% |
| 30/1000 | 3/100 | 0,03 | 3% |
| 130/10 | 13/1=13 | 13,0 | 1300% |
| 8/14 | 4/7 | 4 : 7 = 0,57 | 57% |
2. NALOGA: Na šoli je 750 učencev. Od tega je 58% deklet. Koliko je na šoli deklet in koliko fantov? Nalogo reši na list ali v zvezek.
Na šoli je 435 deklet in 315 fantov.
Na šoli je 470 deklet in 270 fantov.
Na šoli je 435 fantov in 315 deklet.

3. NALOGA: Anže porabi za pot do šole 45 minut. 36 minut se vozi z avtobusom. Koliko odstokov časa hodi peš? Nalogo reši na list ali v zvezek.
80%
66%
40%
20%
120%

4.* NALOGA: Imamo lestev, dolgo 2,5 m. Najprej jo podaljšamo za 20%, nato jo skrajšamo za 20%. Izberi novo dolžino lestve.
2,4 m
2,5 m
2,8 m

5. NALOGA: Vzorec je sestavljen iz več vžigalic. Iz koliko vžigalic je sestavljen niz na
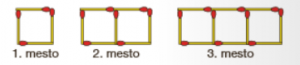
| 5. mestu? | 16 |
| 22. mestu? | 67 |
6. NALOGA: Izračunaj velikost kota β’.
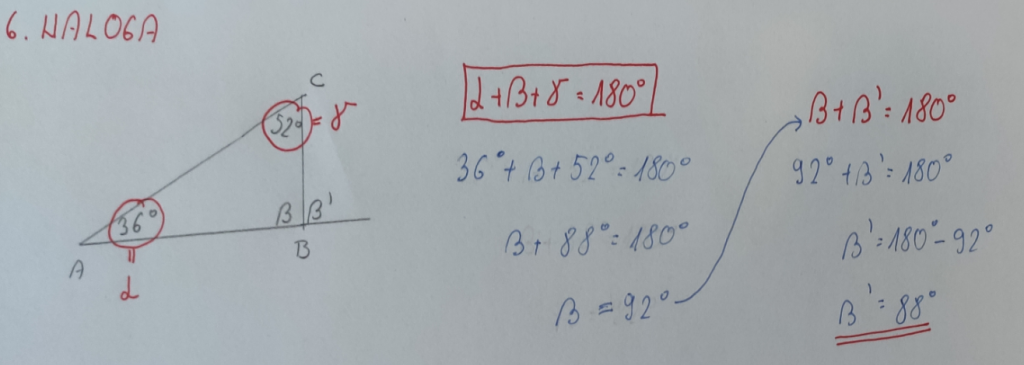
7. NALOGA: Kot β meri:
55°
75°
100°
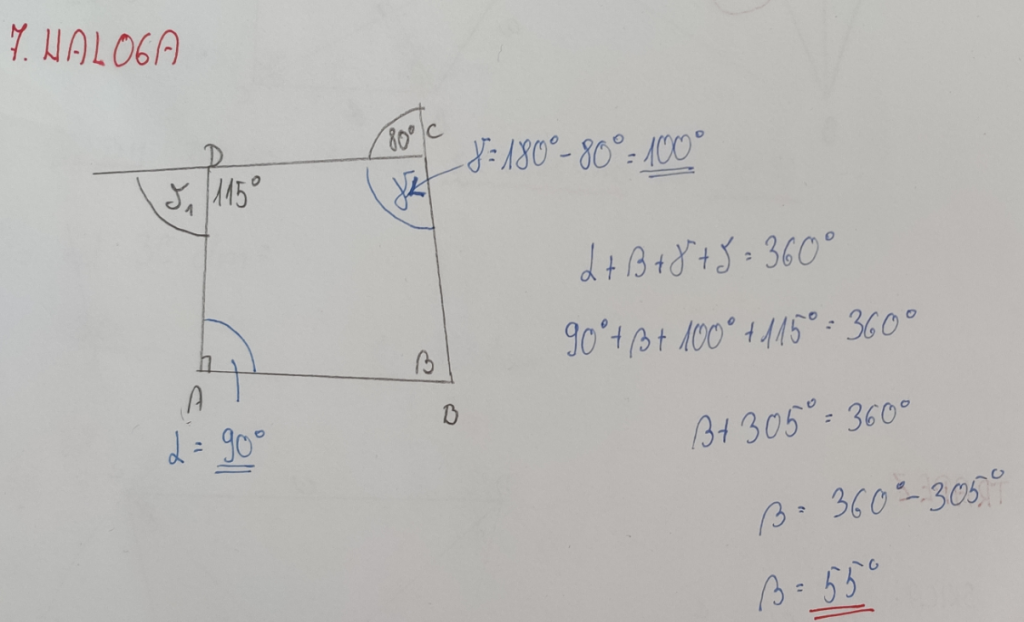
8. NALOGA: Katere od zapisanih izjav so pravilne?
V štirikotniku so lahko vsi štirje notranji koti topi.
Diagonali romba sta skladni.
Vzpredni stranici trapeza imenujemo osnovnici.
Stranice paralelograma so skladne.
Enakokraki trapez in deltoid imata po eno somernico.
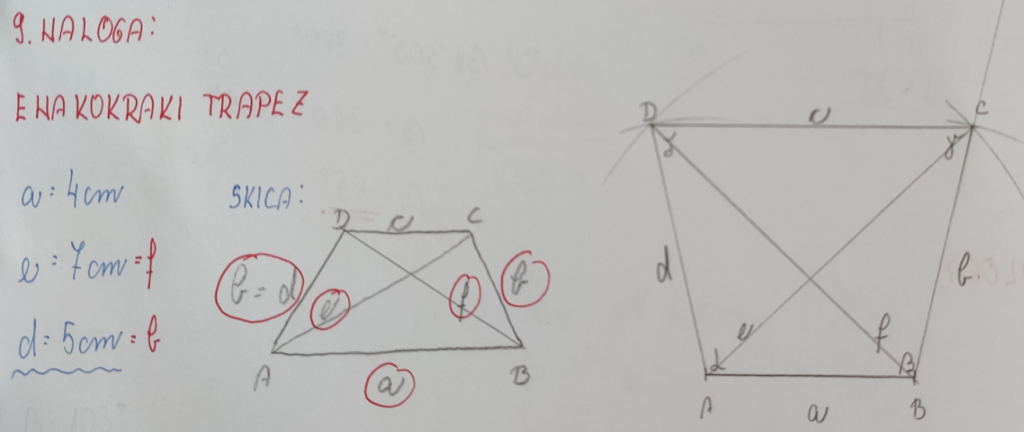
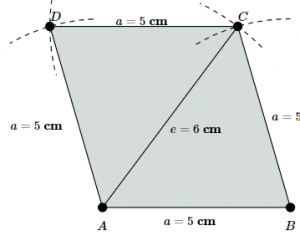
9. NALOGA: Načrtaj enakokraki trapez ABCD s podatki a = 4 cm, e = 7 cm, d = 5 cm. Kot β meri:
42°
76°
104°
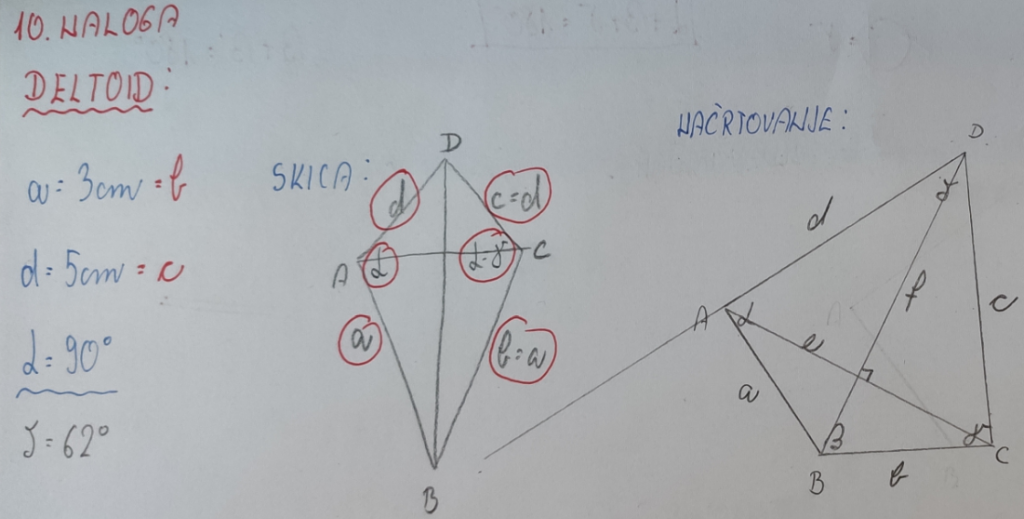
10. NALOGA: Nariši deltoid ABCD s podatki a = 3 cm, d = 5 cm, kot α =90°. Izmeri kot δ in ga zapiši. Skica je obvezna.
7. TEDEN
od 4. 5. do 8. 5. 2020
Dragi učenci!
Ponovno smo nazaj. Upam, da ste se spočili, uživali in si nabrali nove energije. V tednu, ki sledi, bomo ure namenili ponavljanju in utrjevanju snovi.
Čaka vas tudi preverjanje snovi in hkrati priprava na ocenjevanje. O natančnem poteku ocenjevanja boste obveščeni.
1.URA: Ponedeljek 4. 5. 2020
PREVERJANJE ZNANJA PRED OCENJEVANJEM
1.V tej anketi boš preveril svoje znanje o ODSTOTKIH, ENAČBAH, VZORCIH, ZAPOREDJIH, TRIKOTNIKIH in ŠTIRIKOTNIKIH. Anketa je namenjena preverjanju znanja pred ocenjevanjem. Čas za reševanje imaš do petka, 8. 5. 2020, do 14.00. Naloge reši v zvezek. Rešitve bodo objavljene v petek, 8. 5. 2020, od 17.00 naprej.
V nadaljevanju sledita dve uri utrjevanja štirikotnikov, zato ti svetujem, da mogoče najprej rešiš vaje, nato pa preverjanje.
2. Povezava do preverjanja znanja: https://www.1ka.si/a/27794
3. Kriteriji uspešnosti (Kaj bom moral znati za ocenjevanje znanja?)
- ODSTOTKI:
- Odstotki
- Izražanje dela celote v odstotkih.
- Računanje dela celote.
- Računanje celote.
- ENAČBE:
- Izrazi s spremenljivkami.
- Enačbe in njena rešitev.
- Neenačba in množica rešitev.
- VZORCI IN ZAPOREDJA:
- Zaporedja oblik
- Zaporedja števil
- TRIKOTNIKI:
- Označevanje, delitev glede na stranice in kote.
- Koti v trikotniku.
- ŠTIRIKOTNIKI:
- Opis, poimenovanje in delitev.
- Koti v štirikotniku
- Načrtovanje štirikotnikov
- Lastnosti in načrtovanje trapeza.
- Lastnosti in načrtovanje paralelograma.
- Vrste in načrtovanje paralelogramov
- Lastnosti in načrtovanje deltoida.
2. URA: sreda 6. 5. 2020
ALI SI ŽE MOJSTER
Najprej si oglej spodnji video, ki sem ga pripravila za vas. Na posnetku so rešene, ter razložene naloge iz poglavja Ali si že mojster? Odpri DZ 7, 4. del, na strani 130 in reši naloge.
3. URA: četrtek 7. 5. 2020
PONOVIMO ZNANJE O ŠTIRIKOTNIKIH
1. V zvezek napiši naslov.
2. Za vas sem pripravila povzetek celotne snovi o štirikotnikih:
- miselni vzorec o delitvi štirikotnikov,
- tabelo z lastnostmi štirikotnikov.
3. Miselni vzorec in tabelo si prepiši v zvezek (Tukaj si lahko odpreš tudi wordov dokument, ki si ga lahko natisneš in prilepiš v zvezek.)
4. Lastnosti štirikotnikov se nauči. Svetujem ti, da se lastnosti ne učiš se na pamet, ampak s pomočjo skice.
a) DELITEV ŠTIRIKOTNIKOV:
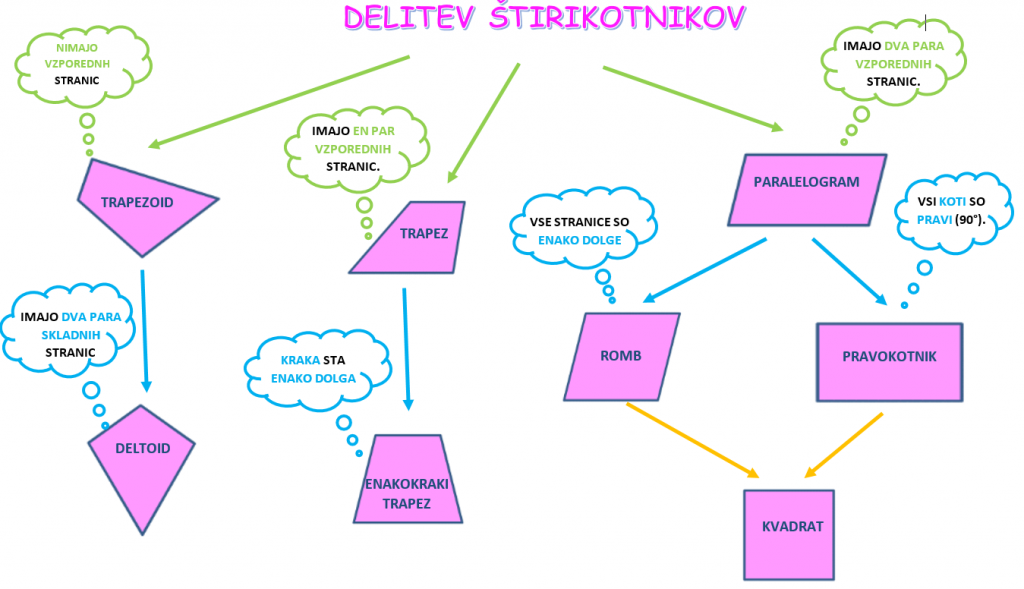
b) LASTNOSTI ŠTIRIKOTNIKOV:
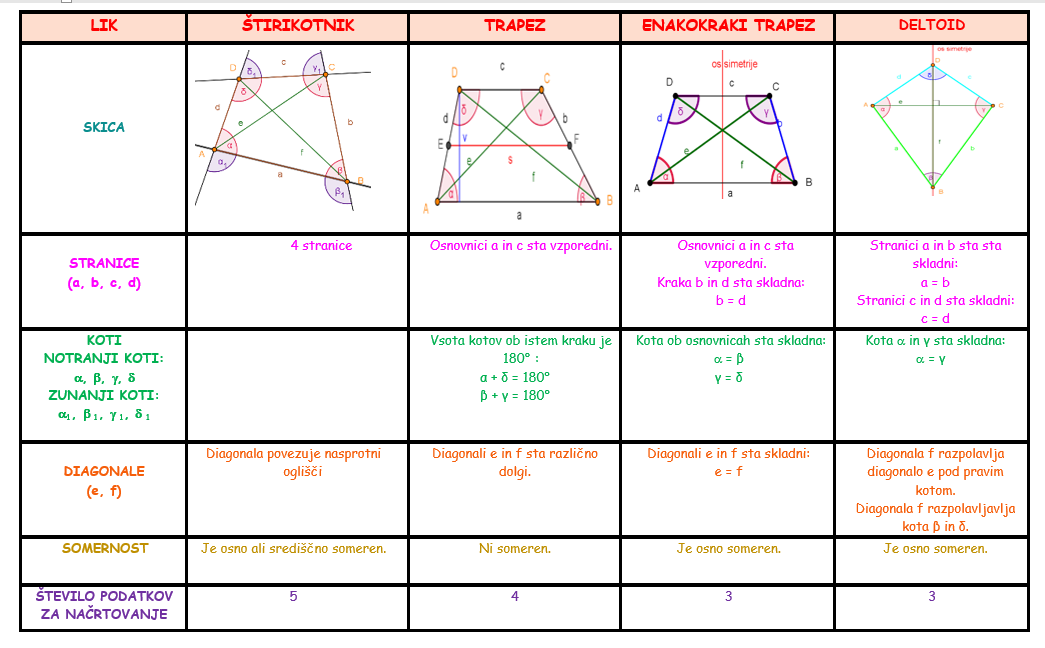
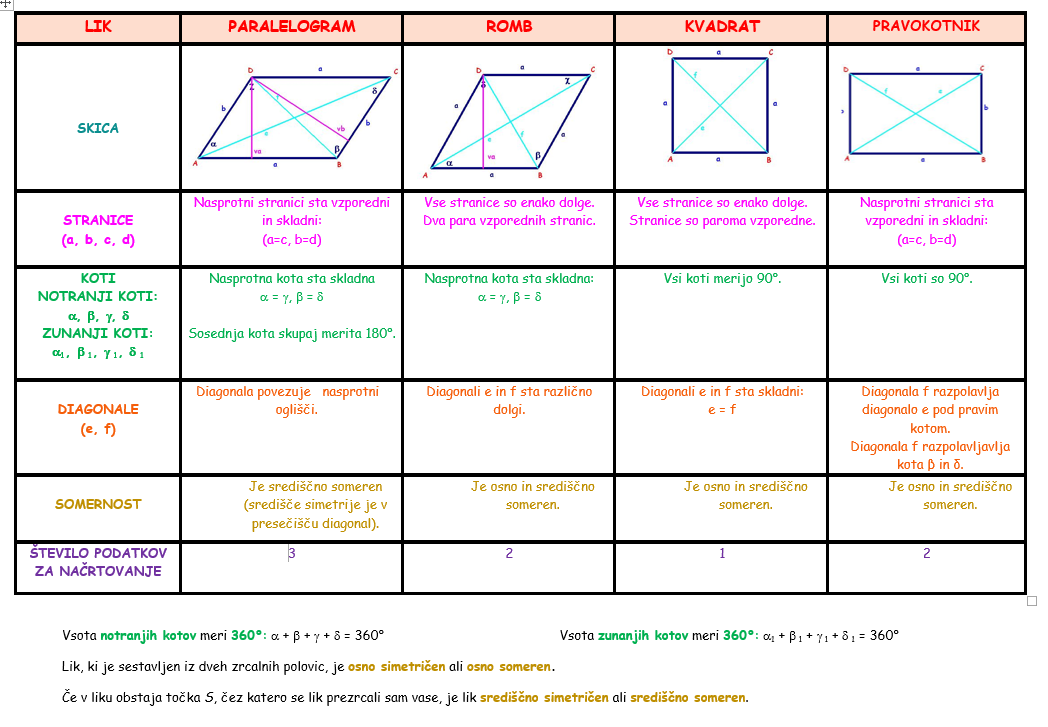
5. V DZS, 4. del na strani 124 reši vsaj naslednje naloge: 2, 3. 5, 6*, 9*, 11, 12, 14. a, 16 in preveri rešitve.
*Nalogi, označeni z zvezdico, sta zahtevnejši in nista obvezni za vse učence.
Kdor zmore, lahko reši še kakšno dodatno nalogo.
________________________________________________________________________________________________________________________
Dragi učenci!
Pred vami so težko pričakovane počitnice. Spočijete si, naberiti si nove energije in uživajte v naravi z družinskimi člani. Če še niste uspeli opraviti vseh anket ali bi snov utrjevali, so vse ankete ponovno odprte.
1. ANKETA: https://www.1ka.si/a/265225
Rešitve: Štirikotniki_rešitve preverjanja
2. ANKETA: https://www.1ka.si/a/269192
Rešitve: Trapez_rešitve preverjanja
3. ANKETA: https://www.1ka.si/a/271945
Rešitve: Paralelogram_rešitve preverjanja
4. ANKETA: https://www.1ka.si/a/274251
Rešitve: Vrste paraleologramov_rešitve preverjanja
Kmalu po počitnicah začnemo z ocenjevanjem znanja. S podrobnejšimi informacijami o načinu ocenjevanja boste seznanjeni.
Uživajte!
MATEMATIČNI KENGURU: Kdor bi želel reševati naloge iz Matematičnega kenguruja preteklih let, jih najdete tukaj.
6. teden od 20. 4. do 24. 4. 2020
ANALIZA 4. ANKETE
- Anketo je rešilo 77 od 95 učencev, to je 81 % vseh učencev.
- 54% učencev je odgovorilo, da snov dobro razume, 43 % delno.
- 82% učencev je rešilo vse naloge, ter 15% učencev je naloge rešilo delno.
- Delež rešitev po nalogah:
- 1. nalogo je pravilno rešilo 34% vseh učencev.
- 2. nalogo je pravilno rešilo 68% vseh učencev.
- 3. nalogo je pravilno rešilo 77% vseh učencev.
- 4. nalogo je pravilno rešilo 76% vseh učencev.
- 5. nalogo je pravilno rešilo 85% vseh učencev.
- 6. nalogo je pravilno rešilo približno 74%vseh učencev.
- 7. nalogo je pravilno rešilo približno 67% vseh učencev.
- 12% učencev meni, da so naloge pretežke, 89% učencev meni, da so naloge ravno prav težke in 0% učencev meni, da so naloge prelahke.
- Odgovori na nekatera vaša vprašanja oz trditve:
– Ali za arnes potrebujem geslo?
Ne, za ogled videoposnetka ne potrebujete gesla. Le kliknete na posnetek.
– Pri načrtovanju pravokotnika je dan podatek, da je stranica d dolga 3 cm. Ali je prav, če uporabimo podatek, da je stranica b dolga 3 cm?
Prav je, da uporabimo b = 3 cm, saj sta stranici b in d skladni pri pravokotniku in sta zato tudi dolžini enaki.
– Kaj pomeni d pri 5. nalogi, diagonala ali višina?
Pri dani nalogi imamo dane podatke za pravokotnik. Mi v pravokotniku ponavadi ne označujemo stranice d, ampak obe pokončni stranici označimo z b. Vendar moramo pri tem poznati lastnosti pravokotnika, torej stranica d je enaka stranici b. Je pa tudi res, da je dolžina stranice d hkrati tudi višina. Vendar višino označujemo s črko v. Diagonale pa označujemo s črkama e in f.
– Zakaj anketa ni veljavna do petka?
Anketa je veljavna štiri dni. Snov v anketi je povezana s snovjo preteklega tedna in ne tekočega tedna. Torej lahko anketo izpolnite že v začetku tedna kot utrjevanje pretekle snovi. V petek pa si pregledate rešitve.
POMEMBNO: Kdor nalog ni opravil in oddal anket, lahko to stori do 30. 4. 2020. Vse ankete bodo ponovno odprte. Isto anketo lahko rešite tudi večkrat in s tem utrdite svoje znanje.
VRSTE PARALELOGRAMOV IN NAČRTOVANJE PARALELOGRAMOV
Rešitve 4. preverjanja
Naloge in rešitve (s skicami in potekom načrtovanja) v word dokumentu lahko najdete tukaj, kjer si jih lahko natisnete in prilepite v zvezek. Sicer pa si rešitve prepišite v zvezek.
1. Naloga: Katerea lika ni na sliki?
Paralelograma
Trapeza
Pravokotnika
Romba
Kvadrata (če ste izmerili stranice, ste opazili, da stranice niso skladne oz. enako dolge)
2. Naloga: Katera trditev velja za kvadrat?
Možnih je več odgovorov.
Diagonali razpolavljata kote ob ogliščih.
Ima diagonali, ki se sekata pod pravim kotom.
Za načrtovanje potrebujemo dva podatka.
Je romb.
Ni središčno someren lik.
3. Naloga: Katera trditev velja za pravokotnik?
Možnih je več odgovorov.
Je osno in središčno someren lik.
Se diagonali medsebojno razpolavljata.
Notranji koti niso skladni.
Je paralelogram.
Se diagonali sekata pod pravim kotom.
4. Naloga: Katera trditev velja za romb?
Možnih je več odgovorov.
Ima po dve nasprotni stranici vzporedni.
Vse notranje kote ima skladne.
Je enakostranični paralelogram.
Ima diagonali, ki nista pravokotni druga na drugo.
Lahko ga načrtamo že z dvema podatkoma.
5. Naloga: Nariši pravokotnik s podatki a = 6 cm, d = 3 cm. Diagonala e meri:
6 cm
6, 7 cm
7, 2 cm
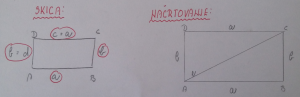
POTEK NAČRTOVANJA:
- Narišemo stranico a in na krajiščih označimo oglišča A in B.
- V oglišču A pravkotno na stranico a narišemo stranico d. Enako naredimo v oglišču B, saj je stranica d skladna stranici b, torej enako dolga. Označimo oglišči C in D.
- Povežemo oglišiči C in D, ter označimo stranice.
- Narišemo diagonalo in jo zmerimo.
6. Naloga: Nariši romb s podatki a = 4 cm, f = 6 cm. Kot β meri:
83°
90°
97°

POTEK NAČRTOVANJA:
- Narišemo stranico a in na krajiščih označimo oglišča A in B.
- V oglišču A s šestilom odmerimo dolžino stranice d (d = a) in narišemo lok.
- V oglišču B s šestilom odmerimo dolžino diagonale f in narišemo lok. Kjer se oba loka sekata, dobimo odlišče D.
- Povežemo oglišči A in D.
- V oglišču D narišemo vzporednico stranici a, ter v oglišču B narišemo vzporednico starnici d (d = a)
- Izmerimo kot β.
7. Naloga: Kot gama meri?
50°
65°
130°
1.URA (PON., 20. 4.):
UTRJEVANJE: Klikni na dano povezavo https://www.1ka.si/a/274251 in reši anketo.
POMEMBNO: Anketo rešite do četrtka 23. 4. 2020. V petek pa si oglejte rešitve analize, ter preverite rešitve preverjanja.
POZNAVANJE NOVE SNOVI:
DELTOID IN LASTNOSTI DELTOIDA
Oglej si posnetek video predstavitve, ki sem ga pripravila za vas. V zvezek si prepiši vsebino, ki je v video predstavitvi ali v zapiskih, ki sledijo.
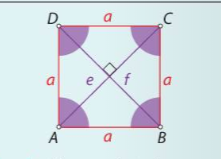
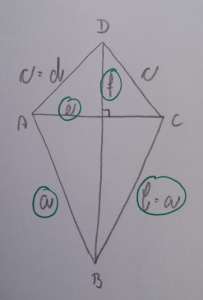
Deltoid je štirikotnik, ki ima dva para skladnih stranic. Spada med trapezoide.
LASTNOSTI DELTOIDA: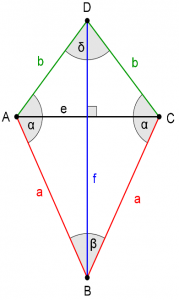
- Je osno someren. Simetrijska os poteka po diagonali f.
- Stranice: a in b sta skladni (a = b), c in d sta skladni (c = d)
- Diagonala f razpolavlja diagonalo e pod pravim kotom.
- Kota α in γ sta skladna (α = γ) .
VAJA: Ugotovi ali je trditev pravilna (P) ali nepravilna (N).
- Deltoid je središčno someren lik.
- Diagonali se sekata pod pravim kotom.
- Diagonali se medsebojno razpolavljata.
- Diagonali razpolavljata notranje kote.
- Ima en par skladnih kotov.
- Ima somernico, ki poteka po eni diagonali.
- Ima dva para skladnih stranic.
- Ima skladni diagonali.
- Vsak pravokotnik je deltoid.
- Vsak kvadrat je deltoid.
- Vsak deltoid je enakostraničen.
REŠITVE: 1. N, 2. P, 3. N, 4. N, 5. P, 6. P, 7. P, 8. N, 9. N, 10. P, 11. N
NALOGE:
V DZ 4, na straneh od 117 do 120 reši vsaj naslednje naloge 2, 4.a, 5, 6 in 10, ter preveri rešitve.
DODATNE NALOGE:
Tisti, ki zmorete lahko rešite še dodatne naloge: 7, 8 in 11.
2.URA (SRE., 22. 4.):
SPOZNAVANJE NOVE SNOVI:
NAČRTOVANJE DELTOIDA
Oglej posnetek video predstavitev, ki sem ga pripravila za vas. V zvezek si prepiši vsebino, ki je v video predstavitvi ali v zapiskih, ki sledijo.
Za načrtovanje deltoida potrebujemo tri podatke.
- PRIMER:
PODATKI:
a = 4 cm
α =120°
f = 6 cm
SKICA:
NAČRTOVANJE:
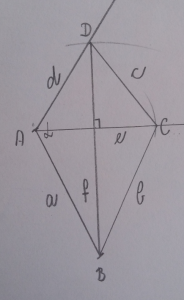
- Narišemo stranico a in v krajiščih stranice označimo oglišči A in B.
- V oglišču A odmerimo kot in iz oglišča A narišemo poltrak.
- Iz oglišča B s šestilom odmerimo dolžino diagonale f in narišemo lok. Kjer se poltrak in lok sekata, dobimo oglišče D. Narisali smo trikotnik ABD.
- Trikotnik ABD prezrcalimo čez diagonalo f.
- Narisanemu deltoidu označimo manjkajoča oglišča, stranice in diagonale.
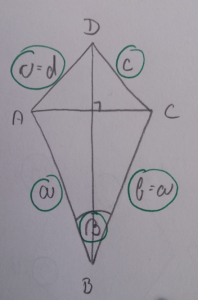
2. PRIMER:
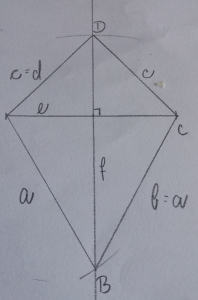
PODATKI:
a = 3 cm
d = 5 cm
β = 110°
SKICA:
NAČRTOVANJE:
- Narišemo stranico a in v krajiščih označimo oglišči A in B.
- V oglišču B odmerimo kot β in iz oglišča B narišemo poltrak, na katerem odmerimo stranico b (3 cm).
- Oglišči A in C povežemo z daljico in dobimo diagonala e.
- Diagonalo e razpolovimo in pravokotno na njo narišemo nosilko diagonale f.
- Iz oglišča A s šestilom odmerimo dolžino daljice d.
- Kjer se lok in nosilka diagonale f sekata označimo oglišče D.
- Povežemo oglišče D in C, označimo oglišča in stranico c.
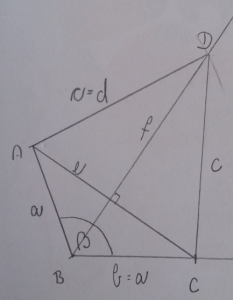
3. PRIMER:
PODATKI:
a = 5 cm
e = 6 cm
f = 7 cm
SKICA:
NAČRTOVANJE:
- Narišemo diagonalo e in na krajiščih označimo oglišči A in C.
- Na polovici diagonale e pravokotno narišemo nosilko diagonale f.
- Iz oglišča A s šestilom odmerimo razdaljo stranice a in narišemo lok na nosilki diagonale f
- Kjer se lok in nosilka diagonale f sekata označimo oglišče B. Povežemo oglišči A in B.
- Iz oglišča B odmerimo razdaljo diagonale f na nosilki diagonale f in dobimo oglišče D. Povežemo oglišča A in D.
- Povežemo oglišči B in C, ter oglišči C in D, ter označimo stranice in diagonale.
NALOGE:
V DZ 4, na straneh od 120 do 122 reši vsaj naslednje naloge 12 a, b, c, d ter preveri rešitve.
DODATNE NALOGE:
Tisti, ki zmorete lahko rešite pri 12 nalogi še ostale primere.
_________________________________________________________________________________________
5. teden, od 14. 4. 2020 do 17. 4. 2020
ANALIZA 3. ANKETE
- Anketo je rešilo 86 od 95 učencev, to je 92 % vseh učencev. Pohvalila bi 7.a in 7.b razred, saj so vsi učenci rešili preverjanje. Naj bo to motivacija še za ostala dva razreda. Verjamem, da zmorete 7.c in 7.d.
- 52% učencev je odgovorilo, da snov dobro razume, 45 % delno in 2 % učencev snovi ni razumelo.
- 80% učencev je rešilo vse naloge, ter 17% učencev je naloge rešilo delno.
- Delež rešitev po nalogah:
1. nalogo je pravilno rešilo 87% vseh učencev.
2. nalogo je pravilno rešilo 84% vseh učencev.
3. nalogo je pravilno rešilo 82% vseh učencev.
4. nalogo je pravilno rešilo 64% vseh učencev.
5. nalogo je pravilno rešilo 64% vseh učencev.
6. nalogo je pravilno rešilo približno 53%vseh učencev.
7. nalogo je pravilno rešilo približno 62% vseh učencev.
- 15% učencev meni, da so naloge pretežke, 82% učencev meni, da so naloge ravno prav težke in 4% učencev meni, da so naloge prelahke.
- Odgovori na nekatera vaša vprašanja oziroma trditve:
– Ali je rešitev pri zadnji nalogi nepravilna?
Prišlo je do napake in je bila rešitev res nepravilna. Napaka je bila takoj, ko ste me opozorili, odpravljena. Hvala za opozorilo.
– Lažje bi bilo, če bi imeli video predavanja.
Za naslednji teden bodo pripravljena video predavanja in upam, da vam bo lažje razumeti snov.
– Zadnja naloga je pretežka.
Vedno je kakšna zahtevnejša naloga za boljše učence.
– Zanima me ali je dovolj končni izgled ali je potrebno slikati vsak korak načrtovanja?
Dovolj je, če slikate skico in končno sliko načrtovanja.
- Opombe na poslane slike:
– Oznako za višino na stranico a označite z oznako va in ne le z v ali a.
– Narisani liki morajo biti označeni z oglišči in stranicami, ter ostalimi danimi podatki. Poslali ste mi kar nekaj fotografij, na katerih so bile slike pomanjkljivo označene.
– Skice:
* Še vedno pogrešam skice. Ko pošiljate slike, mi prosim slikajte še skico.
* Skica naj bo narisana v obliki lika, ki ga načrtujete (v našem primeru je bil to paralelogram) in ne v obliki poljubnega štirikotnika.
* Na skici naj bodo dani podatki obkroženi.
Paralelogram in načrtovanje paralelograma
Rešitve 3. preverjanja
Naloge in rešitve (s skicami in potekom načrtovanja) v word dokumentu lahko najdete tukaj, kjer si jih lahko natisnete in prilepite v zvezek. Sicer pa si rešitve prepišite v zvezek.
- Kaj je paralelogram?
a) Štirikotnik, ki ima dva para vzporednih stranic.
b) Štirikotnik, ki ima en par vzporednih stranic.
c) Štirikotnik, ki ima vse stranice vzporedne.
d) Štirikotnik, ki nima vzporednih stranic.
- Kateri od narisanih likov so paralelogrami?
Možnih je več odgovorov.
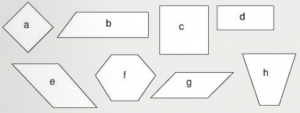
Pravilni odgovori: a, c, d, e, g
- Izberi vse pravilne trditve o paralelogramu.
Možnih je več odgovorov.
Za načrtovanje paralelogram potrebujemo tri neodvisne podatke.
Diagonali paralelograma se razpolavljata.
Vsota notranjih kotov paralelograma je 180°.
Nasprotna kota paralelograma sta skladna.
Diagonali paralelograma sta vedno pravokotni.
- Nariši paralelogram s podatki a = 6 cm, b = 3 cm in α = 60°. Kot β meri:
a) 60°
b) 30°
c)120°
SKICA:
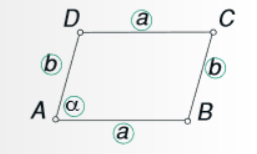
NAČRTOVANJE:
POSTOPEK NAČRTOVANJA:
- Narišemo stranico a in označimo oglišči a in b.
- V oglišču a odmerimo kot α.
- Narišemo stranico b in označimo oglišče d.
- Skozi točko d narišemo vzporednico k stranici a.
- Skozi točko b narišemo vzporednico k stranici b.
- Vzporednici se sekata v oglišču C.
V paralelogram nariši višino na stranico a (va) in jo izmeri. Višina je dolga:
a) 2,6 cm
b) 3 cm
c) 5,2 cm
- Izračunaj notranje kote paralelograma in jih zapiši v spodnjo tabelo.
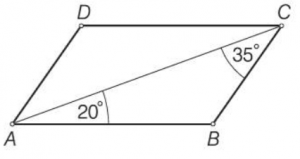
Nasprotna kota v paralelogramu α in γ sta skladna (α = γ):
α = (35° + 20°) = 55°, γ = (35° + 20°) = 55°
Tudi β in δ sta skladna (β = δ). Vsota notranjih kotov je enaka 360°:
α + β + γ + δ = 360°
55° + β + 55° + δ = 360°
β + δ + 110° = 360°
β + δ = 360 – 110° β = δ
β + β = 250°
2 × β = 250°
β = 125° , δ = 125°
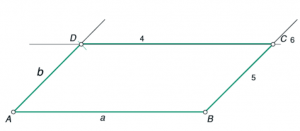
- Nariši paralelogram s podatki f = 5 cm, va = 2 cm in β = 110°. Stranica a meri:
a) 3,8 cm
b) 4,5 cm
c) 5,3 cm
SKICA:
NAČRTOVANJE:
POTEK NAČRTOVANJA:
- Narišemo nosilko stranice a. Na njej poljubno izberemo oglišče B.
- Iz oglišča B odmerimo kot β.
- Narišemo pravokotnico na nosilko stranice a in na njej odmerimo višino na stranico a.
- Skozi krajišče višine narišemo vzporednico k nosilki stranice a.
- V presečišču vzporednice in kraka kota β je oglišče C.
- Iz oglišča B s šestilom odmerimo diagonalo f, ki seka vzporednico v oglišču D.
- Narišemo vzporednico k stranici BC skozi točko D in dobimo oglišče A.
1.URA (TOR., 14. 4.):
Besedila, zapisana ležeče, ni potrebno prepisovati.
UTRJEVANJE: Klikni na dano povezavo https://www.1ka.si/a/271945 in reši tretje preverjanje znanja.
SPOZNAVANJE NOVE SNOVI:
VRSTE PARALELOGRAMOV
Pretekli teden smo že spoznali delitev paralelogramov:
- poševnokotni paralelogrami (paraleleogram in romb)
- pravokotni pralelogram (pravokotnik in kvadrat)
Če želimo načrtovati dane like, moramo dobro poznati njihove lastnosti. Preberi si lastnosti likov v spodnji tabeli in vsako lastnost preveri v skici. Nato si tabelo prepiši v zvezek (lahko pa jo tudi natisneš. Klikni na “Delitev paralelogramov“).
| POŠEVNOKOTNI | PRAVOKOTNI | |
|
R A Z N O S T R A N I Č N I
|
PARALELOGRAM je štirikotnik, ki ima dva para vzporednih stranic.
LASTNOSTI PARALELOGRAMA: – Nasprotni stranici ima vzporedni in skladni (a = c, b = d). – Nasprotna kota sta skladna (a = g, b =d). – Nima pravih kotov. – Sosednja kota skupaj merita 180°. – Je središčno someren lik. – Diagonali paralelograma se razpolavljata. |
PRAVOKOTNIK je paralelogram in ima vse njegove lastnosti.
LASTNOSTI PRAVOKOTNIKA: – ima dva para različno dolgih stranic (b =d, a = c), – vse notranje kote ima prave (90°), – diagonali sta skladni (e =f) in se razpolavljata. – je osno in središčno someren. |
|
E N A K O S T R A N I Č N I |
ROMB je paralelogram, ki ima vse štiri stranice skladne (enako dolge).
LASTNOSTI ROMBA: – Ima enako dolge (skladne), paroma vzporedne stranice: |AB| = |BC| = |CD| = |AD| = a (vse stranice označujemo s črko a, saj so vse enako dolge) – Diagonali romba e in f: o razpolavljata notranje kote romba (Diagonala e razpolavlja kota a in γ, diagonala f razplavlja kota β in δ.), o sta med sabo pravokotni (e⊥f) in se razpolavljata. – Je središčno in osno somern lik. |
KVADRAT je enakostraničen (vse stranice so enako dolge) in pravokoten (vsi notranji koti merijo 90°) paralelogram.
LASTNOSTI KVADRATA: – Je pravokotnik in romb in ima vse njune lastnosti. – Ima enako dolge, paroma vzporedne stranice. – Diagonali kvadrata e in f (Pazi: V kvadratu pogosto diagonale označimo tudi s črko d.): o sta enako dolgi (e = f). o Se sekata pod pravim kotom. o razpolavljata kote ob ogliščih, o sekata se pravokotno (e⊥f). – Je osno in središčno someren lik. |
DODATNA RAZLAGA NA VIDEOPOSNETKIH (za tiste, ki niste razumeli vseh lastnosti paralelogramov):
PRAVOKOTNIK: https://astra.si/pravokotnik/
ROMB: https://astra.si/romb/
KVADRAT: https://astra.si/kvadrat/
PRIMER: Trditve si zapiši v zvezek in najprej reši sam (pomagaj si z zgornjo tabelo), nato preveri rešitve in napačne popravi.
Katera trditev je pravilna?
- Romb je paralelogram.
- Paralelogram je štirikotnik z enim parom vzporednih stranic.
- Paralelogram je središčno someren lik.
- Romb je osno someren lik.
- Nasprotni stranici paralelograma sta skladni in vzporedni.
- Kvadrat je paralelogram.
- V paralelogramu se diagonali sekata pravokotno.
Rešitve:
- Romb je paralelogram. P
- Paralelogram je štirikotnik z enim parom vzporednih stranic. N (z dvema paroma vzporednih stranic)
- Paralelogram je središčno someren lik. P (središče v presečišču diagonal)
- Romb je osno someren lik. P
- Nasprotni stranici paralelograma sta skladni in vzporedni. P
- Kvadrat je paralelogram. P
- V paralelogramu se diagonali sekata pravokotno. N (v splošnem paralelogramu ne, v ROMBU in KVADRATU pa sta diagonali pravokotni)
VAJA: V SDZ 4 na str. 103 – 113 reši vsaj naslednje naloge: 1, 2, 7, 11, 13 in preveri rešitve.
DODATNE NALOGE: Kdor zmore, lahko reši še dodatne naloge v SDZ 4 na str. 103 – 113: 3, 8, 15, 16, 17 in preveri rešitve.
2. URA (SRE., 15. 4.):
NAČRTOVANJE PARALELOGRAMOV
Za načrtovanje romba in pravokotnika potrebujemo dva podatka, za načrtovanje kvadrata pa le enega.
NAČRTOVANJE:
Pri načrtovanju različnih paralelogramov zopet upoštevamo enak vrsti red načrtovanja, kot pri že obravnavanih likih:
1) Izpišemo podatke (Ker bomo načrtovali različne paralelograme, nad podatki zapišemo ime paralelograma):
ROMB:
a = 5 cm
e = 6 cm____
2) Narišemo skico ( na njej označimo vsa oglišča in stranice, ter vse ostale podatke, ki so dani) in obkrožimo dane podatke.
Dano imamo stranico a. Če poznamo lastnosti romba,
potem velja, da so vse stranice enake: a = b = c = d.
Torej na skici označimo vse stranice s črko a.
3) Načrtovanje lika:
POTEK NAČRTOVANJA:
- Narišemo stranico a in označimo oglišča A in B.
- Iz oglišča A odmerimo krožni lok z dolžino diagonale e = 6 cm.
- Iz oglišča B odmerimo krožni lok z dolžino stranice a = 5 cm.
- Kjer se loka sekata, označimo oglišče C.
- Iz oglišča A in C odmerimo dolžino stranice a = 5 cm.
- Kjer se loka sekata označimo oglišče D.
- Povežemo vsa oglišča in označim stranice in diagaonalo e.
VAJA: Reši vsaj naslednje naloge v DZ 4, str. 105:
- 5. a, c, e (če primera e ne znaš, si oglej rešen primer v DZ 4 na str. 102),
- 9. a (pri pravokotniku upoštevaj njegove lastnosti. Skica naj bo narisana kot pravokotnik),
- 21. a, b (NAMIG: Omenili smo, da diagonale pri kvadratu največkrat označimo tudi s črko d).
Preveri rešitve.
DODATNE NALOGE: Kdor zmore, lahko reši še dodatno nalogo in sicer naloge:
- 5. b (za pomoč, si lahko ogledaš spodnji rešen primer), č,
- 9. b, c (za pomoč, si lahko ogledaš rešen primer v DZ 4 na str. 108)
PRIMER K DODATNI NALOGI:
1) Izpišemo podatke:
ROMB:
a = 4 cm
v = 3 cm____
2) Narišemo skico in obkrožimo dane podatke:
3) Narišemo dani lik:
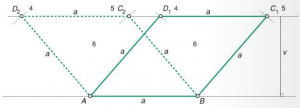
POTEK NAČRTOVANJA:
- Narišemo stranico a in označimo oglišči A in B.
- Narišemo pravokotnico na naosliko stranice a in odmerimo višino romba.
- Skozi krajišče višine narišemo vzporednico k nosilki a.
- Iz oglišča A s šestilom odmerimo stranico a in na vzporednici dobimo dve presečišči, ki ju označimo z D1 in D2.
- Iz oglišča B s šestilom odmerimo stranico a in na vzporednici dobimo dve presečišči, ki ju označimo s C1 in C2.
- Povežemo oglišča obeh dobljenih rombov, saj ima naloga dve rešitvi.
_________________________________________________________________________________________
Navodila za reševanje anket:
– takšen način preverjanja bo sledil vsak teden,
– k reševanju pristopite resno, saj s tem preverite razumevanje snovi,
– je za vse učence obvezen,
– povratne informacije o vašem sodelovanju in razumevanju snovi si bomo beležili,
– pri reševanju so vam lahko v pomoč zvezki, učbeniki …,
– anketa bo aktivna do četrtka,
– povratne informacije oz. rešitve nalog bodo objavljene v petek na spletni strani za posamezen razred,
– povezavo do anket boste našli na spletni strani pri posameznem razredu.
V kolikor potrebujete dodatne informacije ali imate vprašanja, pišite tukaj. Z veseljem vam bomo pomagali.
Uspešno delo še naprej in ostanite zdravi.
Učitelji matematike
_________________________________________________________________________________________
4. teden, od 6. 4. 2020 do 10. 4. 2020
2. PREVERJANJE ZNANJA:
Dragi učenci, po vaših odzivih in rešenih nalogah v preverjanju sklepam, da vam gre vedno bolje, kar me veseli. S skupnimi močmi nam bo zagotovo uspelo. Drugo preverjanje znanja je za vami. Zelo sem vesela vašega odziva pri reševanju preverjanja.
Pri pregledu rešenih preverjanj, sem opazila nekaj pogosto storjenih napak, na katere vas bom opozorila v nadaljevanju:
IZPIS PODATKOV IN SKICA:
V poslanih fotografijah je manjkalo veliko skic ali pa so bili dani podatki na skici neobkroženi. Upoštevajte navodila, ki smo jih zapisali, pri spoznavanju načrtovanja trapeza (izpisani podatki, narisana skica in obkroženi dani podatki).
Skica naj bo v obliki trapeza, ki ga načrtujete in ne v obliki poljubnega štirikotnika. Tako, lahko že iz skice ugotovite lastnosti, ki vam bodo olajšale načrtovanje (npr. iz pravilno narisane skice, lahko razberete, da sta kraka b in d enako dolga in to lastnost upoštevate pri načrtovanju).
MERJENJE KOTOV:
Pri zadnji nalogi je bilo iz fotografij razvidno, da je trapez načrtan prvilno, izmerjena velikost kota pa nepravilna. Namesto zunanje skale na geotrikotniku, ste prebrali notanjo skalo (npr. namesto 110°, ste prebrali 70°), zaradi tega pa prišli do nepravilne rešitve. Na to bodite zelo pozorni. Pri podobnih nalogah lahko sklepate tudi iz slike, da je načrtan kot večji od pravega kota (90°), torej izmerjeni kot nikakor ne more biti velik 70°.
NATANČNOST PRI NAČRTOVANJU:
Nekatere vzporednice, koti in stranice so bile načrtane nenatančo. Če se dolžina stranic ali velikost kota razlikuje le za dva mm ali dve stopinju od pravilne rešitve, je rešitev žal napačna. Zato bodite res natančni pri načrtovanju.
Za natančno načrtovanje želim, da uporabljate:
- šestilo, ki se ne premika med načrtovanjem in ima ostro konico,
- ošiljen svinčnik,
- geotrikotnik z nepoškodovanim robom in številkami.
Naj vam bodo te napake v opomin, da jih pri utrjevanju in obravnavi nove snovi ne ponovite in s tem nalogo rešite pravilno, ter dobite motivacijo za nadaljno delo.
Veliko vas je celoti pravilno rešilo anketo, zato vam čestitam in le tako naprej. Ostalim pa naj bo to motivacija za nadaljna preverjanja, ki sledijo. Bodite še naprej vztrajni in pogumni pri reševanju nalog, delu in učenju.
Želim vam še naprej uspešno delo, ostanite zdravi in lepe praznike!
REŠITVE 2. PREVERJANJA:
Naloge in rešitve (s skicami in potekom načrtovanja) v word dokumentu lahko najdete tukaj, kjer si jih lahko natisnete in prilepite v zvezek. Sicer pa si rešitve prepišite v zvezek.
- Kaj je trapez?
- Trapez je štirikotnik, ki ima nasprotni stranici vzporedni.
- Trapez je štirikotnik, ki nima vzporednih stranic.
- Trapez je štirikotnik, ki ima vse prave kote.
- Trapez je štirikotnik, ki ima dve stranici vzporedni.
- Izberi trditev, ki velja za trapez.
- Diagonali se razpolavljata.
- Notranja kota ob istem kraku trapeza merita skupaj 180°.
- Pravokotno razdalja med nosilkama obeh osnovnic imenujemo srednjica trapeza.
- Je osno someren lik.
- Izberi trditev, ki velja za enakokraki trapez.
- Ima dva para vzporednic.
- Kota ob osnovnicah sta enako velika.
- Diagonali sta skladni.
- Je središčno someren lik.
- Za načrtovanje trapeza potrebujemo
- 3 podatke.
- 4 podatke.
- 5 podatkov.
- Za načrtovanje enakokrakega trapeza potrebujemo
- 3 podatke.
- 4 podatke.
- 5 podatkov.
- Načrtaj trapez s podatki a = 6 cm, b = 3 cm, c = 2, 5 cm in β = 60°. Stranica d meri:
*Pri načrtovanju se lahko zmotiš za največ 2 mm.
- 3 cm
- 3,4 cm
- 2,5 cm
Skico, načrtovanje in potek načrtovanja poglej v dani prilogi (če klikneš na besedo “tukaj”).
7.Nariši enakokraki trapez s podatki c = 3 cm, d = 4 cm, f = 6 cm. Izmeri kot δ in zapiši njegovo velikost.
Skico, načrtovanje in potek načrtovanja poglej v dani prilogi (če klikneš na besedo “tukaj”).
Odgovor: Velikost kota δ je 117°.
1. URA: PON (6.4.2020):
UTRJEVANJE:
Klikni na dano povezavo https://www.1ka.si/a/269192 in reši anketo.
SPOZNAVANJE NOVE SNOVI:
PARALELOGRAM in LASTNOSTI PARALELOGRAMA
Na povezavi: https://astra.si/paralelogram/ si oglej videoposnetek.
Najprej preberi, nato prepiši spodnje lastnosti v zvezek. Kar je zapisano ležeče, ti ni potrebno prepisovati. Tukaj so zapiski v Wordu, si ki jih lahko natisneš n prilepiš v zvezek.
PARALELOGRAM je štirikotnik, ki ima dva para vzporednih stranic (skico si preriši DZ 3, str. 94 ali iz dodane datoteke (zgoraj), če klikneš na besedo “Tukaj”)
A,B,C,D…oglišča
a, b, c, d…stranice
a, b, g, d…notranji koti
e, f… diagonali
va, vb…. višini
LASTNOSTI PARALELOGRAMA:
- Nasprotni stanici ima vzporedni in skladni (a = c, b = d).
- Nasprotna kota sta skladna.
- Sosednja kota skupaj merita 180°.
- Kota ob isti osnovnici sta suplementarna.
- Je središčno someren Središče simetrije je v presečišču diagonal.
- Diagonali paralelograma se razpolavljata.
- Višina paralelograma je pravokotna razdalja med vzporednima stranicama trikotnika. (Višine lahko rišemo tudi znotraj paralelograma. Pomembno je, da je višina pravokotna na stranico-obvezno označimo pravi kot)
RAZVRSTITEV PARALELOGRAMOV:
- poševnokotni paralelogrami (paraleleogram in romb)
- pravokotni paralelogram (pravokotnik in kvadrat)
V DZ 3 na strani 93 si oglej spodnjo tabelo in preberi kaj velja za dane like.
VAJA:
V SDZ 3 na str. 96 -98 reši vsaj naslednje naloge: 2 b, č, 3, 5, 7 b, c, č*, 8 in preveri rešitve.
2. URA: SRE (8.4.2020):
NAČRTOVANJE PARALELOGRAMA
Posamezne lastnosti o paralelogramu, ki smo se jih naučili preteklo uro, moramo upoštevati tudi pri načrtovanju poljubnih paralelogramov. Pomembno je, da poznate lastnosti vseh likov, zato se jih je potrebno naučiti in razumeti. Če jih boste znali, ne boste imeli težav pri načrtovanju.
Za načrtovanje paralelograma potrebujemo tri neodvisne podatke.
Potek načrtovanja paarleogramov: (verjetno ste opazili, da je pri načrtovanjih vseh likov enak potek načrtovanja iin tudi oznake ogljišč, stranic, kotov, ….so vedno za vse štirikotnike enaki)
- najprej izpišemo podatke ,
- narišemo skico (skico nariši v oblik paralelograma)
- označimo vsa ogljišča in stranice, ter vse ostale dane podatke
- obkrožimo dane količine,
- razmislimo v kakšnem vrstnem redu bomo načrtovali paralelogram
- pričnemo načrtovanje.
PRIMER:
Na strani 94, reši 2. nalogo. Nariši skico ter načrtaj dani paarlelogram. Postopka načrtovanja ni potrebno pisati.
Če načrtovanje paralelograma še vedno ne razumeš, si lahko ogledaš še naslednja dva videoposnetka: risanje paralelograma 1 (https://www.youtube.com/watch?v=DsMXmmxXNtA), risanje paralelograma 2 (https://www.youtube.com/watch?v=4azb1o8N1Xk). Boljši učenci si lahko ogledate še mal zahtevnejši primer risanja paralelograma 3 (https://www.youtube.com/watch?v=OFGvkyjKKbk).
VAJE:
V delovnem zvezku DZ 4, str. 98 – 100, reši vsaj naslednje naloge: 9.b, c (PAZI: pri tem primeru sta dve možni rešitvi), č, d f*, g* (naloge z zvezdico rešijo boljši učenci) in preveri rešitve. Kote riši s kotomerom in ne s šestilom, kot je v navodilu naloge.
_________________________________________________________________________________________________________________________
3. teden, od 30. 3. 2020 do 3. 4. 2020
ANALIZA 1. ANKETE:
Dragi učenci!
Reševanje prve ankete je za vami. Hvala vsem, ki ste sodelovali. Bi pa opomnila učence, ki ankete niste izpolnili, da jih v prihodnje redno izpolnjujete, saj so obvezne za vse učence.
V nadaljevanju sledijo odgovori na vprašanja in dileme, ki ste jih zapisali pri reševanju anket. Odgovori so namenjeni vsem učencem. V njih mogoče najdete odgovor na vprašanje, ki ste si ga tekom dela na daljavo, zastavili in si nanj niste znali odgovoriti. Hkrati pa vas pozivam, da svoja vprašanja in dileme napišete tudi v prihodnjih anketah. Z veseljem vam bom odgovorila.
Odgovori na vprašanja in dileme:
Vprašanja in dileme so kopirane iz ankete.
- jaz vedno mešam gamo in delto. To se bo pa treba zapomnit: γ (gama), δ (delta). Mogoče nasvet: zapiši si ju na listek in ga prilepi na računalnik, da ju boš vsak dan opazil-a. Ne dvomim, da ti ne bo uspelo. Srečno!
- želim si še več takšnih nalog. Vedno lahko narediš še vse ostale naloge, ki jih nismo uspeli v tem poglavju. Če ti jih je še vedno premalo, dodatne najdeš na povezavi: https://eucbeniki.sio.si/matematika7/783/index.html,
- nove snovi naj so lepše označene-razporejene po razredih. Je že urejeno po razredih. Verjamem, da bo sedaj lažje najti razred.
- kaj naj se naredim oz preberem da bom boljše razumela? Lahko si pomagaš s to spletno povezavo: https://eucbeniki.sio.si/matematika7/783/index.html, kjer najdeš dodatno razlago, animacije, vaje z rešitvami,…. Lahko pa mi tudi pišeš in mi zastaviš vprašanje, ki ti dela težave. Z veseljem ti pomagam.
- nisem razumel katere razlage pri 5. vprašanju? Pri vprašanju »Česa nisi razumel?« je bilo mišljeno, katere snovi, tekom dela od doma, nisi razumel oz. kje si imel težave.
REŠITVE 1. PREVERJANJA:
Naloge in rešitve (s skicami) v word dokumentu lahko najdete tukaj, kjer si jih lahko natisnete in prilepite v zvezek. Sicer pa si rešitve prepišite v zvezek.
- Ugotovi ali je trditev pravilna ali nepravilna.
| Da | Ne | |
| Štirikotnik je telo. | X Štirikotnik je lik. | |
| Štirikotnik ima 4 točke, 4 daljice in 4 kote. | X | |
| Vsota notranjih kotov je 360°. | X | |
| Kota ob isti stranici sta nasprotna. | X Kota ob isti stranici sta sokota. | |
| Vsota zunanjih kotov v štirikotniku je enaka vsoti notranjih kotov v štirikotniku. | X | |
| Za načrtovanje štirikotnika potrebujemo štiri neodvisne podatke | X Za načrtovanje štirikotnika potrebujemo pet neodvisnih podatkov. |
- Velikosti treh zunanjih kotov štirikotnika ABCD so 57°, 108° in 103°. Izračunaj velikost četrtega zunanjega kota.
REŠEVANJE: Vsota vseh treh kotov skupaj je 57° + 108° + 103° =268°. Vsota vseh zunanjih kotov je 360°. Torej od 360° odštejemo vsoto ostalih treh kotov: 360° – 268° = 92°.
ODGOVOR: Velikost četrtega kota je 92°.
- Izračunajte velikost neznanih kotov β in γ v štirikotniku, če je α =125°, β1 = 99°, δ = 67°. Pomagaj si s skico.
ODGOVORI:
– Kota merita 91° in 87°
– Kota merita 69° in 81°
– Kota merita 81° in 87°
- Določi pravilen vrstni red načrtovanja štirikotnika s podatki a = 4 cm, c = 6 cm, d = 4 cm, e = 7 cm in
f = 7 cm. Pomagaj si s skico. Možnih je več odgovorov
ODGOVORI:
– Stranica a, stranica d, diagonala f, stranica c, diagonala e.
– Stranica a, diagonala f, stranica d, stranica c, diagonala e.
– Stranica c, stranica d, diagonala e, stranica a, diagonala f.
– Stranica c, stranica a, diagonala e, stranica d, diagonala f.
– Stranica a, diagonala f, diagonala e, stranica c, stranica d.
- Nariši štirikotnik s podatki b = 4 cm, c = 6 cm, d = 2,5 cm, β = 75°, γ = 90°. Izmeri dolžino stranice a in jo zapiši.
ODGOVOR: Možni sta dve rešitvi. Stranica a lahko meri 6 cm ali 7,6 cm.
_________________________________________________________________________________________________________________________
1.URA: Ponedeljek (30.3.2020):
UTRJEVANJE: Zgoraj si preberi navodila za reševanje anket. Nato klikni na sledečo povezavo: https://www.1ka.si/a/265225 in izpolni anketo.
SPOZNAVANJE NOVE SNOVI:
TRAPEZ IN LASTNOSTI TRAPEZA
Na povezavi: https://astra.si/trapez/ si oglej videoposnetek. Preberi in prepiši spodnje lastnosti in načrtovanje trapeza v zvezek. Tukaj so zapiski v wordu, ki si jih lahko natisneš in prilepiš v zvezek..
Trapez je štirikotnik, ki ima en par vzporednih stranic (skico si preriši iz dodane datoteke, če klikneš na besedo “Tukaj”) .
A,B,C,D…oglišča
a, b, c, d…stranice
e,f …diagonali
v…višina
s…srednjica
Lastnosti trapeza:
- je štirikotnik, ki ima en par vzporednih stranic: a in c, ki jih imenujemo osnovnici,
- nevzporedni stranici b in d sta kraka,
- pravokotna razdalja med nosilkama osnovnic je višina trapeza (ima samo eno višino, saj ima samo en par vzporednih stranic)
- daljica, ki veže nasprotni oglišči je diagonala trapeza, diagonali e in f sta različno dolgi.
- srednjica (s) je daljica, ki povezuje razpolovišči obeh krakov in je vzporedna z osnovnicama. Srednjica razpolavlja višino trapeza. Izračunamo jo z enačbo: ,
- vsota velikosti notranjih kotov trapeza je 360° (α+ β+γ +δ =360°),
- vsota velikosti kotov ob istem kraku je enaka iztegnjenemu kotu (α+δ=180°, β+γ=180°).
ENAKOKRAKI TRAPEZ je trapez, ki ima oba kraka skladna (a=b).
Lastnosti enakokrakega trapeza:
Skico si preriši iz dodane datoteke, če klikneš na besedo “Tukaj”.
– je osno someren lik,
– kraka b in d sta enako dolga (b=d),
– kota ob osnovnici sta skladna (a=β in γ=δ),
– diagonali sta skladni (e =f),
– somernica razpolavlja osnovnici a in c.
VAJE:
V delovnem zvezku DZ 4, str. 84 – 87, reši vsaj naslednje naloge: 3., 4., 5., 6, 9. a, 10. b in preveri rešitve.
2. URA: Sreda (1.4.2020):
NAČRTOVANJE TRAPEZA
Za načrtovanje trapeza potrebujemo štiri neodvisne podatke. Za načrtovanje enakokrakega trapeza potrebujemo le tri podatke.
Potek načrtovanja trapezov:
- najprej izpišemo podatke,
- narišemo skico
- označimo vsa oglišča in stranice, ter vse ostale dane podatke
- obkrožimo dane količine,
- razmislimo v kakšnem vrstnem redu bomo načrtovali trapez
- pričnemo načrtovanje (Glej, da boš imel-a ošiljen svinčnik, ustrezno šestilo in geotrikotnik)
PRIMERI:
Na straneh 81- 83, reši naloge: 2, 3 in 4. Obvezno nariši skico ter načrtaj dani trapez, postopka načrtovanja ni potrebno pisati.
Če načrtovanje trapeza še vedno ne razumeš, si lahko ogledaš še naslednja dva videoposnetka: risanje trapeza 1 (https://www.youtube.com/watch?v=NFdLtSoYfPg), risanje trapeza 2 (https://www.youtube.com/watch?v=tvXeFj-mgzI)
VAJE:
V delovnem zvezku DZ 4, str. 87 – 92, reši vsaj naslednje naloge: 11.b, č, d, 13, 14 b in 15.a in preveri rešitve.
_________________________________________________________________________________________________________________________
2. teden, od 23. 3. 2020 do 27. 3. 2020
1. IN 2. URA: 23. 3. 2020 IN 25.3. 2020:
NAČRTOVANJE ŠTIRIKOTNIKA
ZAPIS V ZVEZEK – tukaj si zapis lahko tudi natisneš (dodane so še skice …)
Za načrtovanje štirikotnikov potrebujemo pet neodvisnih podatkov.
Potek načrtovanja štirikotnikov:
- najprej izpišemo podatke,
- narišemo skico ( rišemo jo s prosto roko, skica naj ne bo premajhna), označimo oglišča, stranice in dane kote, ter obkrožimo podane količine,
- razmislimo v kakšnem vrstnem redu bomo načrtovali štirikotnik (postopek načrtovanja pišemo le pri spoznavanju nove snovi, pri utrjevanju ga ne pišemo)
- pričnemo načrtovanje.
Načrtovanje štirikotnikov, če imamo dane:
a) STRANICE IN KOTE:
Na spletni strani https://eucbeniki.sio.si/matematika7/783/index1.html si oglej ZGLED, v zvezek nariši skico ter načrtaj dani štirikotnik.
PRIMER: V delovnem zvezku DZ 4, str. 76 – 77, reši nalogo 1.a in 1.c
b) STRANICE IN DIAGONALE:
Na spletni strani https://eucbeniki.sio.si/matematika7/783/index2.html si oglej ZGLED, nariši skico, ter načrtaj dani štirikotnik.
PRIMER: V delovnem zvezku DZ 4, str. 76, reši nalogo 1.b.
c) STRANICE, DIAGONALI IN KOTI:
Na spletni strani https://eucbeniki.sio.si/matematika7/783/index3.html si oglej ZGLED, nariši skico, ter načrtaj dani štirikotnik.
PRIMER: V delovnem zvezku DZ 4, str. 77 – 78, reši nalogo 1.e in 1.f
VAJA:
V DZ 4, str. 77 – 79, reši 1. č, d, 2. in preveri rešitve.
_________________________________________________________________________________________________________________________
1. teden, od 16. 3. 2020 do 20. 3. 2020
7. r
Navodila za samostojno učenje matematike v 7. r v tednu od 16. do 20. marca 2020.
Utrjevanje odstotkov
- Reši naloge z učnega lista (Odstotki_vaje_z_rešitvami).
- Naloge rešuj v zvezek.
- Za reševanje nalog uporabi enega izmed postopkov, ki smo se ga učili v šoli in ti je najlažji. Piši postopek reševanja.
- Naloge z zvezdico so priporočljive za boljše učence.
- Preveri rešitve in jih popravi.
Štirikotnik
- Preberi snov v delovnem zvezku (4. del) za 7. r, na straneh 66 – 67 . OPOMBA – učenci 7. d snov le ponovijo.
- V zvezek zapiši naslov in kratek povzetek (opis štirikotnika, vrste štirikotnikov, odnos stranic in kotov štirikotnikov)
- V delovnem zvezku reši vsaj naslednje naloge:
DZ4, str. 67 – 68, naloge 2 – 6.
Ustno odgovori na vprašanja na strani 66: Z mojstrom do znanja.
Koti v štirikotniku
- Preberi snov v delovnem zvezku (4. del) za 7. r na strani 70 – 71.
- V zvezek zapiši naslov in kratek povzetek (vsota notranjih in vsota zunanjih kotov).
- Na spletni strani: https://eucbeniki.sio.si/matematika7/781/index2.html s premikanjem oglišč štirikotnika in spreminjanjem velikosti kotov, lahko preveriš vsoto notranjih in zunanjih kotov.
- Reši zgled 3. v delovnem zvezku.
- V delovnem zvezku reši vsaj naslednje naloge:
DZ4, str. 72 – 74, naloge 1, 2, 3, 4 a
Ustno odgovori na vprašanja na strani 70: Z mojstrom do znanja.