Urednik strani: Franci Kravcar, za vsa vprašanja se obrnite na e-naslov: franci.kravcar@os-trebnje.si

NOVO – V ponedeljek, 25. 5. 2020, prinesti s seboj Samostojni delovni zvezek št. 3 in 5.

F. Kravcar

Tukaj lahko preverite ocene pisnega preizkusa.

Tukaj lahko dostopate do zahtevnejših nalog (matematični kenguru …).

Spoštovani učenci,

za vas sem zbral vse ankete z rešitvami, tudi nove ankete bodo na tem mestu. Povezave so spodaj. Če vam razrednik sporoči, da nisi opravil ankete, vendar si jo oddal, me prosim obvesti preko e-pošte.

• 7. anketa – ocenjevanje znanja
  • rešitve
    
• 6. preverjanje znanja, 11. 5. 2020
  • rešitve
• 5. preverjanje znanja, 4. 5. 2020
  
  • rešitve
• 4. preverjanje znanja, 20. 4. 2020
  
  • rešitve 
• 3. preverjanje znanja, 13. 4. 2020
  
  • rešitve
• 2. preverjanje znanja, 7. 4. 2020
  
  • rešitve
• 1. preverjanje znanja, 1. 4. 2020
  
  • rešitve

Rešitve domačih nalog

Spoštovani učenci,

nekateri učenci ste izrazili željo, da objavim tudi rešitve domačih nalog. Od sedaj naprej bodo rešitve nalog dostopne tudi na spletni strani.

• NOVO – Rešitve domačih nalog za 9. teden (rešene so le obvezne naloge, če kdo ni razumel zahtevnejših nalog, naj mi piše po e-pošti)
  
• Rešitve domačih nalog 8. tedna (11. 5.-15.5.2020), Površina stožca, SDZ 5, od str. 6 do str. 26

________________________________________________________________________________

9. TEDEN, 18. 5.-22. 5. 2020

POMEMBNO – PISNI PREIZKUS ZNANJA – NAVODILA

V torek, 19. 5. 2020, bomo od 11.00 do 12.00 preko sistema 1ka pisali pisni preizkus – anketo iz matematike, tokrat za oceno. Učenci, ki imate podaljšan čas pisanja, boste lahko reševali anketo do 12.15.

Nekaj nalog bo potrebno tudi slikati in oddati kot priponko k anketi.

Pisni preizkus je obvezen za vse, ki v 2. ocenjevalnem obdobju še nimate ocene. Ocena, ki ste jo nekateri učenci pridobili s popravljanjem negativne ocene, ne nadomesti ocene v 2. oc. obdobju.

Ostali učenci boste imeli na anketi vprašanje ali želite, da sem vam anketa oceni ali ne. Če bo odgovor da, se anketa oceni, sicer ne. Ocena, ki jo boste pridobili, bo bolj informativne narave. Zaključevalo se bo pretežno na podlagi preteklih ocen.

Učenci, ki ste bili do 16. marca med oceno, pa bo ta ocena lahko vplivala na zaključevanje (navzgor/navzdol).

Če se kdo skupnega ocenjevanja ne bo udeležil, pa nujno potrebuje oceno, bo pozvan k ocenjevanju  preko aplikacije Zoom. Po 25. maju bo lahko vprašan tudi v šoli. Enako velja, če bo pisal negativno.

Verjamem, da boste reševali pošteno in pokazali svoje realno znanje. Če pa bom vseeno sumil na goljufijo, bom pozval vse učence, ki bi bili lahko vpleteni, k zagovoru.

Vsebine, ki se bodo preverjale:

• PRIZMA, SDZ 3, od str. 105 do str. 141
• PRIZMA, SDZ 4, od str. 5 do str. 51
• VALJ, SDZ 4, od str. 52 do str. 94
• PIRAMIDA, SDZ 4, od str. 95 do str. 157
• STOŽEC, SDZ 5, od str. 5 do str. 23
• OBDELAVA PODATKOV, SDZ 5, od str. 77 do str. 144

Priporočam vam, da še enkrat rešite vse ankete in pregledate zapiske in naloge, ki ste jih dobili za domače delo.

ponedeljek, 18. 5. 2020

V tem tednu bomo spoznali:

• 1. ura, SDZ 5, str. 24, Prostornina stožca
  
• 2. ura,  SDZ 5, str. 37, Enakostranični stožec
  

__________________________________________________________________________

1. ura, ponedeljek, 18. 5. 2020

Prostornina stožca

SDZ 5, str. 24

Najprej si oglej spodnji video, ki sem ga pripravil.

Zapiski, ki morajo biti v zvezku.

Prostornina stožca

1. ura, ponedeljek, 18. 5. 2020

1. Prostornina stožca

Prostornina stožca je enaka tretjini produkta ploščine osnovne ploskve in višine.

Zgledi

Rešili bomo naloge v SDZ 5 od str. 26 naprej: 1., 4., 6., 8., 12. in 14. č naloga.

(Najprej jih reši, potem preveri rešitve spodaj. Naloge rešuj v delovni zvezek, zato tukaj ne bo navodil, le rešitve).

1. naloga, str. 26

4. naloga, str. 27

6. naloga, str. 27

8. naloga, str. 28

12. naloga, str. 29

14. č) naloga, str. 32

Samostojno delo

• Reši naloge, naloge z zvezdico so dodatne: SDZ 5, od str. 26 naprej/2. naloga, 2. tabela; 7., 9., 11., 14. c*, 19.*, 20.*, 21.**

__________________________________________________________________________

2. ura, sreda, 21. 5. 2020

Enakostranični stožec

Najprej si oglej spodnji video, ki sem ga pripravil.

Zapiski, ki morajo biti v zvezku.

Enakostranični stožec

 

2. ura, sreda, 21. 5. 2020

1. Opis

Enakostranični stožec ima stranico enako premeru osnovne ploskve. Osni presek enakostraničnega stožca je enakostranični trikotnik.

Zgledi

Rešili bomo naloge v SDZ 5 od str. 39 naprej: 1., 4. in 5. naloga.

(Najprej jih reši, potem preveri rešitve spodaj. Naloge rešuj v delovni zvezek, zato tukaj ne bo navodil, le rešitve).

1. naloga, str. 39

4. naloga, str. 40

5. naloga, str. 40

 

______________________________________________________________________

8. TEDEN, 11. 5.-15. 5. 2020

Rešitve 6. ankete

sobota, 16. 5. 2020

 

ANALIZA ANKETE

• Anketo je v roku ustrezno rešilo 64 učencev ali 77 % vseh učencev.
  

Opomba

Vsem učencem, ki niso ustrezno rešili ankete (brez priponke, nisem mogel odpreti priponke, naloge so bile pretežno napačno rešene …) sem poslal e-sporočilo, v katerem sem pozval te učence k dopolnitvi rešitev.

Odgovori na nekatera vaša vprašanja:

• Nekaterih anket še nisem opravil. Kje lahko dobim informacijo o tem?
  • Če niste prepričani, katerih anket še niste opravili, mi pišite na e-naslov: franci.kravcar@os-trebnje.si.
• Te snovi ne razumem, nihče mi ne more pomagati …
  • V primeru, da snovi ne razumete, pojdite še enkrat skozi video predavanja, rešitve nalog (ankete, domače naloge …), vprašajte sošolca, lahko tudi mene …
• Rok za oddajo bi bil lahko podaljšan do nedelje, da bi lahko naloge rešili čez vikend.
  • Predlog je “na mestu”, bom razmislil o njem.

Kar nekaj učencev je pohvalilo količino domačih nalog, video razlago … Tudi to le lepo prebrati :).

6. preverjanje znanja – rešitve, OPIS STOŽCA, POVRŠINA STOŽCA

1. naloga

Ploščina osnovne ploskve stožca meri 13 dm², njegova površina pa 56 dm².

Koliko meri njegov plašč?

 

2. naloga

Ploščina plašča stožca meri 60 dm², njegova površina pa 3,7 m².

Koliko meri njegova osnovna ploskev?

3. naloga

Ploščina osnovne ploskve stožca meri 10 dm², njegov plašč pa je šestkrat večji od osnovne ploskve. Koliko m² meri njegova površina?

 

4. naloga

Izračunaj ploščino plašča, če meri polmer r =3 dm, stranica stožca pa s = 6 dm.

 

5. naloga

Izračunaj površino stožca, če meri premer 24 cm, stranica stožca pa 2 dm. Za pi vzemi 3,14.

 

6. naloga

Izračunaj površino stožca, če meri višina v = 12 dm, stranica stožca pa s = 15 dm. Rezultat naj bo točen. Skica.

7*. naloga

Premer osnovne ploskve stožca meri 18 dm, njegova višina pa 40 dm. Izračunaj ploščino osnega preseka in plašč stožca.

ponedeljek, 11. 5. 2020

POMEMBNO – PISNI PREIZKUS ZNANJA

V torek, 19. 5. 2020, bomo od 11.00 do 12.00 preko sistema 1ka pisali pisni preizkus – anketo iz matematike, tokrat za oceno. Povezava do ankete bo na spletni strani že kakšnem dan prej, aktivna pa bo ob uri pisanja. Pisni preizkus je obvezen za vse učence, ki v 2. ocenjevalnem obdobju še nimajo ocene. Ostali učenci boste imeli na anketi vprašanje ali želite, da sem vam anketa oceni ali ne. Če bo odgovor da, se anketa oceni, sicer ne. Ocena, ki jo boste pridobili, bo bolj informativne narave, zaključevalo se bo pretežno na podlagi preteklih ocen. Učenci, ki ste bili do 16. marca med oceno, pa bo ta ocena lahko vplivala na zaključevanje (navzgor/navzdol). Vsi boste imeli zaradi izrednih razmer podaljšan čas pisanja, 60 minut. Če se kdo skupnega ocenjevanja ne bo udeležil, pa nujno potrebuje oceno, bo lahko pozvan k ocenjevanju  preko aplikacije Zoom. Enako velja, če bo pisal negativno, učitelj podvomi  o verodostojnosti ankete (možnost goljufije) ali ob morebitnih nejasnostih. V primeru, da se vrnemo v šolo, bo lahko opravil razgovor tudi v šoli. Pri pisanju imejte pripravljen tudi fotoaparat ali mobilni telefon, da boste poslali sliko vašega izdelka, v kolikor bo anketa to zahtevala (podobno, kot ste že pripenjali slike do sedaj).

Vsebine, ki se bodo preverjale:

• PRIZMA, SDZ 3, od str. 105 do str. 141
• PRIZMA, SDZ 4, od str. 5 do str. 51
• VALJ, SDZ 4, od str. 52 do str. 94
• PIRAMIDA, SDZ 4, od str. 95 do str. 157
• STOŽEC, SDZ 5, od str. 5 do str. 23
• OBDELAVA PODATKOV, SDZ 5, od str. 77 do str. 144

Priporočam vam, da še enkrat rešite vse ankete in pregledate zapiske in naloge, ki ste jih dobili za domače delo.

V tem tednu bomo začeli zopet z obravnavo nove snovi. Spoznali bomo STOŽEC.

• Razpored učnih ur:
  
  • 1. ura, SDZ 5, str. 6, Opis in vrsta stožca.
    
  • 2. ura,  SDZ 5, str. 13, Plašč in površina stožca
    

__________________________________________________________________________

1. ura, ponedeljek, 11. 5. 2020

Opis in vrste stožca

SDZ 5, str. 6

Najprej si oglej spodnji video, ki sem ga pripravil.

Zapiski, ki morajo biti v zvezku.

Opis in vrste stožca

1. ura, ponedeljek, 11. 5. 2020

1. Opis stožca

Stožec je okroglo geometrijsko telo, ki ga omejujeta ena ravna in ena kriva ploskev ter ima en vrh in en rob

Skica

Osnovna ploskev je krog (ravna ploskev), plašč je krožni izsek (kriva ploskev). Točka V je vrh stožca.

Mreža stožca

Osni presek stožca

Samostojno delo

• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 5, od str. 9 naprej/1., 2., 6., 8., 9, 10., 11.* in 12.*

__________________________________________________________________________

2. ura, sreda, 13. 5. 2020

Plašč in površina stožca

Najprej si oglej spodnji video, ki sem ga pripravil.

Zapiski, ki morajo biti v zvezku.

Plašč in površina stožca

 

2. ura, sreda, 13. 5. 2020

Obrazec za računanje plašča in površine stožca (preriši sliko in prepiši obrazce)

Zgled

(Vse naloge so iz Samostojnega delovnega zvezka, od str. 15 naprej. Naloge rešuj v delovni zvezek, zato tukaj ne bo navodil, le rešitve).

2. naloga, str. 15

5. naloga, str. 16

8. naloga, str. 17 (opomba, v rešitvi manjka pi)

12. a) naloga, str. 19

15. c) naloga, str. 21

Samostojno delo

• Reši naslednje naloge, naloge z zvezdico so dodatne: SDZ 5, od str. 16 naprej/3. naloga, 1. tabela; 4., 9. a, 12. c, 15*. b, 19*., 22.**

______________________________________________________________________

Rešitve 5. preverjanja znanja

sobota, 9. 5. 2020

ANALIZA ANKETE

• Anketo je v roku ustrezno rešilo 65 učencev ali 78 % vseh učencev.
  

Opomba

Učenci, prosim, da si dobro pregledate rešitve še posebej, ker se bliža ocenjevanje, ki bo podobno preverjanju. Kar nekaj učencev je rešilo določene naloge napačno. Vsem učencem, ki niso ustrezno rešili ankete (brez priponke, nisem mogel odpreti priponke, naloge so bile pretežno napačno rešene …) sem poslal e-sporočilo, v katerem sem pozval te učence k dopolnitvi rešitev.

Odgovori na nekatera vaša vprašanja:

• Na posnetku niste povedali, za katero nalogo iz SDZ gre?
  • Bom v bodoče še to dodal, je pa pomembno, kako se rešuje dolčena naloga. Pametno je, da posnetek ustavite, poskusite rešiti nalogo in šele potem preverite rešitev. Tako se boste največ naučili.
• Dva učenca še vedno opozarjata na preveliko količino nalog.
  • Žal manj nalog že težko dam, če želim, da se vsak učni cilj v poglavju vsaj delno utrdi in preveri. Vaju pa razumem, da je veliko predmetov, nalog … poskusite zdržati, še malo, pa bodo počitnice 🙂
• En učenec je napisal, da ničesar ne razume.
  • Temu učencu sem poslal e-sporočilo z navodili za pomoč. Če je še kdo tak, naj poišče pomoč pri sošolcu, naj mi piše, seveda s konkretnimi vprašanji, še enkrat posluša video predavanja, pregleda rešitve anket …

5. preverjanje znanja – rešitve, PRIZMA, PIRAMIDA, VALJ in OBDELAVA PODATKOV

1. naloga

Izračunaj dolžino roba kocke, če meri njena površina 1536 dm2.

2. naloga

Ali je 100 cm2 dovolj za izdelavo škatle z robovi a = 3,2 cm, b = 2,4 cm in c = 6,8 cm? Odgovor utemelji z računom.

3. naloga

Ploščina osnovne ploskve pravilne štiristrane prizme je 20,25 dm2, višina pa meri 9 dm. Koliko meri njena površina in koliko prostornina?

 

4. naloga

Lonec valjaste oblike ima premer 30 cm in je visok 20 cm. Koliko litrov drži  (π=3,14)?

 

5. naloga

Izračunaj ploščino plašča pravilne štiristrane piramide, če meri osnovni rob 6 cm, telesna višina pa 4 cm (skica)?

 

6. *naloga

Ploščina osnovne ploskve pravilne tristrane piramide meri 49 dm2, stranski rob pa 2,5 m. Izračunaj površino piramide. Rezultat zaokroži na dve decimalni mesti natančno.

7. naloga

V vrečki so kroglice. Diagram prikazuje število kroglic glede na barvo.

a) Kolikšna je verjetnost, da iz vrečke na slepo povlečemo belo kroglico?

b) Kolikšna je verjetnost, da na slepo izvlečena kroglica ni niti rdeča niti zelena?

8. naloga

Igralna kocka ima tri ploskve pobarvane rdeče, ena ploskev je bela in 2 ploskvi sta zelene barve.

a) Kolikšna je verjetnost, da pri metu kocke pade zelena barva (rezultat izrazi z okrajšanim ulomkom)?

b) Katero srednjo vrednost lahko določimo barvam ploskev kocke in katera barva je to?

7. TEDEN, 4. 5.-8. 5. 2020

ponedeljek, 4. 5. 2020

V tem tednu se bomo pripravljali na 5. preverjanje znanja, ki zajema PRIZMO, PIRAMIDO, VALJ in OBDELAVO PODATKOV. Zaključilo bomo poglavje o valju in ponovili prizmo ter piramido. Na koncu rešite preverjanje znanja, ki bo osnova (priprava) za vašo oceno pri matematiki.

• Kaj bomo spoznali v tem tednu?
  • 1. ura, SDZ 4, str. 92, Ali si že mojster?
  • 2. ura,  Ponovimo, prizma in piramida.
    

__________________________________________________________________________

1. ura, ponedeljek, 4. 5. 2020

Ali si že mojster?

SDZ 4, str. 92

Najprej si oglej spodnji video, ki sem ga pripravil za vas. Ker gre predvsem za razlago nalog priporočam, da posnetek pri vsaki nalogi ustavite, poskusite rešiti nalogo sami, potem primerjate rešitev.

Samostojno delo

• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 4, od str. 92 naprej/1., 3., 4., 5., 2.*, 6.*, 7.* in 8.*

__________________________________________________________________________

2. ura, sreda, 6. 5. 2020

Ponovimo

Prizma in Piramida

Najprej si oglej spodnji video, ki sem ga pripravil za vas. Ker gre predvsem za razlago nalog priporočam, da posnetek pri vsaki nalogi ustavite, poskusite rešiti nalogo sami, potem primerjate rešitev.

Zapiski, ki morajo biti v zvezku.

Ponovimo

Prizma in Piramida

2. ura, sreda, 6. 5. 2020

Zgled

a) Izračunaj površino prizme, če meri osnovna ploskev 25 cm2, plašč pa 120 cm2.

b) Izračunaj osnovno ploskev in prostornino prizme, če meri površina 700 cm2, plašč 230 cm2 in višina 14 cm.

 

c) Izračunaj površino in prostornino prizme, ki je predstavljena na sliki.

č) Izračunaj površino in prostornino prizme, ki je predstavljena na sliki.

d) Površina pravilne štiristrane prizme meri 4888 cm2. Izračunaj njeno višino, če meri osnovni rob 26 cm.

e) Ploščina osnovne ploskve pravilne štiristrane piramide meri 12 dm2, stranske ploskve pa 7,5 dm2.  Koliko meri površina piramide?

f) Osnovni rob pravilne štiristrane piramide meri 8 cm, višina pa 3 cm. Izračunaj površino te piramide.

g) Prostornina  pravilne štiristrane piramide meri 32 cm3. Koliko meri osnovni rob te 6 cm visoke piramide?

 

ZAPOMNI SI

• Prizmo omejujeta dve osnovni ploskvi in plašč.
  

• Površina prizme je enaka vsoti ploščin dveh osnovnih ploskev in plašča (P = 2O + pl).
• Prostornina je enaka produktu osnovne ploskve in višine prizme (V = Ov).
• Piramido omejuje ena osnovna ploskev in plašč.
  

• Površina piramide je enaka vsoti ploščin ene osnovne ploskve in plašča (P = O + pl).
• Prostornina je enaka tretjini produkta osnovne ploskve in višine prizme (V = Ov/3).

Samostojno delo

• Reši 5. preverjanje znanja (anketo), povezava je na začetku.

Rešitve 4. preverjanja znanja – ANKETE, z analizo

petek, 24. 4. 2020

Tukaj  lahko prenesete rešitve.

ANALIZA ANKETE

• Anketo je rešilo 66 učencev (80 %)
•  51 %, učencev je odgovorilo, da snov razume, 44 % delno in 1 učenec snovi ni razumel.
• 85 % učencev je rešilo vse naloge, ki sem vam jih zastavljal iz SDZ
• Večina učencev je odgovorila, da jim video razlaga koristi.
• Delež rešitev po nalogah, posredujem analizo 1., 5., 6. in 7. naloge
  • 1. naloga, 7 učencev je nalogo rešilo napačno, ostali pravilno
    
  • 5. naloga, vsi ste oddali sliko rešitev, vendar vas je nekaj napisalo (4 učenci), da naloge niste razumeli – poglejte si rešitev ali je niste rešili pravilno (5 učencev). Sem pa vesel, da ste ostali čitljivo napisali rešitev  in tudi pravilno rešili.
    
  • 6*. naloga, pravilno jo je rešilo 49 učencev
    
  • 7*. naloga, pravilno jo je rešilo 35 učencev
    
• Odgovori na nekatera vaša vprašanja:
  • Še vedno menim, da je prevelika količina nalog (2 učenca)
    • Verjamem, da ni enostavno. Veliko je vsega, predmetov, predavanj, zapiskov … Vendar ne smete pozabiti, da imate le polovično število ur, naloge so razdeljene po zahtevnosti, lahko kakšno izpustite. Šola mora biti še vedno na prvem mestu. Žal je tudi manj nalog težko dati, ker potem ne boste utrdili vseh ciljev. Bom se pa potrudil, da bom res izbral najnujneše obvezne naloge, še vedno pa bodo dodatne naloge za tiste, ki želite nekaj več.
  • Nekaj nalog nisem razumel …
    • Preglejte rešitve, če še vedno ne bo šlo, priporočam ponovno poslušanje video predavanj, kjer so razložene nekatere naloge.

4. preverjanje znanja – rešitve, Osni presek valja in Ali si že mojster?

1. naloga

Izračunaj ploščino osnega preseka valja, če meri polmer osnovne ploskve 3,5 cm, višina valja pa 11,8 cm. Pri reševanju ne uporabljaj računala.

 

2. naloga

Špela je zapisala besedo MATEMATIKA. Mala Taja s prstom kaže posamezne črke.

• Kolikšna je verjetnost, da bo izmed črk pokazala na črko A?
• Za katere črke je najmanjša verjetnost, da jih bo pokazala, in kolikšna je?
• Pri katerih črkah je verjetnost, da jih bo pokazala, 1/5?

3. naloga

Katera in koliko dvomestnih števil lahko sestaviš iz števk 2, 5, 9, če naj se števke v številu ne ponavljajo? Pomagaš si lahko s kombinatoričnim drevesom.

 

4. naloga

Cene ima ob koncu šolskega leta pri matematiki naslednje ocene: 2, 2, 3, 4, 5, 4, 4. Določi aritmetično sredino (na eno decimalko natančno), modus in mediano danih ocen.

 

5. naloga

Osni presek valja je kvadrat ABCD s ploščino 196 cm². Izračunaj višino valja in ploščino plašča valja. Rezultat naj bo natančen.

 

6. *naloga

Kolikšna je ploščina osnega preseka valja s premerom d = 50 cm in ploščino plašča pl = 420π cm²?

7*. naloga

Izračunaj ploščino plašča valja, če meri površina P = 1 805π cm², razmerje med premerom in višino pa je 4 : 3. Izrazi ploščino plašča in površino s polmerom.

________________________________________________________________________________

6. TEDEN, 20. 4.-24. 4. 2020

ponedeljek, 20. 4. 2020

V tem tednu bomo zopet delali vsi enotno. Obravnavali bomo mešana poglavja. Ena ura bo iz SDZ 5 in ena ura iz SDZ 4. To pa zato, da se vse skupine zopet poenotijo. Dve poglavji bomo izpustili s skupino V. Pirc. Tudi brez teh dveh poglavij se da razumeti in rešiti Ali si že mojster?

Potem se vrnemo na valj (2. ura). Vem, da je skupina V. Pirc poglavje o valju že končala. Nič pa ne bo narobe, če še enkrat ponovite to poglavje :).

• Kaj bomo spoznali v tem tednu?
  • 1. ura, SDZ 5, str. 140, Ali si že mojster?
  • 2. ura, SDZ 4, str. 78, Osni presek valja

__________________________________________________________________________

1. ura, ponedeljek, 20. 4. 2020

Ali si že mojster?

SDZ 5, str. 140

Najprej si oglej spodnji video, ki sem ga pripravil za vas.

Na posnetku je kratka ponovitev celotnega poglavja Obdelava podatkov in rešenih ter razloženih nekaj nalog iz Ali si že mojster? Prav ti bo prišlo pri reševanju nalog :).

Potem se loti reševanja nalog v SDZ 5, str. 140

Samostojno delo

• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 5, od str. 140 naprej/1.-6., 7. a, b** in c, 8. **, 9. in 10.

__________________________________________________________________________

2. ura, sreda, 22. 4. 2020

Osni presek valja

SDZ 4, str. 78

 

Najprej si oglej spodnji video, ki sem ga pripravil za vas.

Zapiski, ki morajo biti v zvezku (spodaj).

Osni presek valja

SDZ 4, str. 78

2. ura, sreda, 22. 4. 2020

Zgled

a) Izračunaj ploščino osnega preseka valja, če meri polmer osnovne ploskve 10 cm, višina valja pa 20 cm.

b) Obseg osnovne ploskve valja je 7π cm, višina valja je 0,4 dm. Izračunaj ploščino osnega preseka.

Reševanje

c) Ploščina osnega preseka enakostraničnega valja je 1296 cm2. Kolikšno površino in kolikšno prostornino ima valj? Rezultat izrazi s številom π.

Reševanje

ZAPOMNI SI

• Osni presek valja je pravokotnik z dolžino, ki je enaka premeru 2r, in širino, ki je enaka višini valja v.
• Osni presek enakostraničnega valja je kvadrat.

Samostojno delo

• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 4, od str. 80 naprej/1. in 3. ali 4. in 10 ter dodatne naloge, 5*, 7* in 9*.

 

________________________________________________________________________________________________________________

5. TEDEN, 14. 4.-17.4.2020

Rešitve 3. preverjanja znanja – ANKETE, z analizo

petek, 17. 4. 2020

Tukaj  lahko prenesete rešitve.

ANALIZA ANKETE

• Anketo je rešilo 66 učencev, to je79,5%.
• 57% učencev je odgovorilo, da snov razume, 40% delno razume snov.
• 90% učencev je rešilo vse naloge v delovnem zvezku, ki sem vam jih predpisal.
• 69% učencev meni, da jim videopredavanje koristi.
• Analiza po nalogah
  • Prvi del nalog je 85% učencev rešilo pravilno.
  • 70% učencev je rešilo tudi težje naloge. Pravilno je bilo rešenih v povprečju 70% nalog.
• Odgovori na nekatera vaša vprašanja
  • Vprašanj ni bilo. Izpostavili pa ste, da vam video posnetki pomagajo pri razumevanju nove snovi.

3. preverjanje znanja – naloge, Valj, Modus in Mediana – rešitve

1. naloga

Izračunaj prostornino valja, če meri premer 42 mm, višina valja pa 3,6 cm.

2. naloga

Izračunaj prostornino in površino enakostraničnega valja, če meri višina valja 54 cm.

3. naloga

Jernej ima pri matematiki ocene 4, 5, 5, 4, 4, 5 in 3. Določi modus ocen pri Jerneju.

4. naloga

Petra ima pri matematiki ocene 2, 4, 5, 3, 4, 3 in 3. Določi mediano ocen pri Petri.

5. *naloga

V valjasto posodo s premerom 9 cm vlijemo 6 decilitrov vode. Kako visoko sega voda v posodi?

6. *naloga

Enakostranični valj ima ploščino plašča 1296π cm2. Koliko meri njegova površina in koliko prostornina?

7*. naloga

Dani so številski podatki 5, 2, 1, 3 in 6. Dodaj manjkajoči podatek tako, da bo mediana 4.

_________________________________________________________________________________________________________________

ponedeljek, 13. 4. 2020

V tem tednu bomo spoznali dve novi učni enoti, je pa odvisno, pri katerem učitelju ste. Na koncu rešite anketo – 3. preverjanje znanja, ki bo vsebovala vsa 4 poglavja.

Kaj bomo spoznali v tem tednu?

• Učenci V. Pirc (ostali ste to že obravnavali):
  • Modus ali gostiščnica
  • Mediana ali središčnica
• Ostali učenci (učenci V. Pirc ste to že obravnavali):
  • Prostornina valja
  • Enakostranični valj

 

Prostornina valja, 1. ura – za učence učitelja F. Kravcarja, K. Slapar in F. Petelinca

SDZ 4, str. 61

torek, 14. 4. 2020

Najprej si oglej spodnji video, ki sem ga pripravil za vas. Po ogledu naredi zapiske, po potrebi lahko še enkrat poslušaš razlago. Nato se loti samostojnega dela.

 

 

Zapiski, ki morajo biti v zvezku.

Prostornina valja

SDZ 4, str. 61

torek, 14. 4. 2020

Zgled

a) Lonec valjaste oblike ima premer 30 cm in je visok 20 cm. Koliko litrov drži?

Reševanje

b) Osnovna ploskev valja ima ploščino 100π cm2, višina valja je 14 cm. Izračunaj prostornino in površino valja.

Reševanje

Zapomni si

• Prostornino valja izračunamo tako, da pomnožimo ploščino osnovne ploskve (kroga) z višino valja.

V = O v

Samostojno delo

• Preberi še razlago v SDZ 5, str. 61.
• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 4, od str. 62 naprej/1, 2, 3, 6, 7*, 18*,24*.

________________________________________________________________________________________________________________________

Enakostranični valj, 2. ura – za učence učitelja F. Kravcarja, K. Slapar in F. Petelinca

SDZ 4, str. 71

sreda, 15. 4. 2020

Najprej si oglej spodnji video, ki sem ga pripravil za vas. Po ogledu naredi zapiske, po potrebi lahko še enkrat poslušaš razlago. Nato se loti samostojnega dela.

Zapiski, ki morajo biti v zvezku.

Enakostranični valj

SDZ 4, str. 71

sreda, 15. 4. 2020

Zgled

a) Premer enakostraničnega valja meri 18 cm. Izračunaj površino in prostornino.

Reševanje

b) Plašč enakostraničnega valja je pravokotnik z višino 16 cm. Izračunaj površino in prostornino valja.

Reševanje

Zapomni si

• Valj je enakostranični, če je višina valja enaka premeru osnovne ploskve.
  

v = 2 r

Samostojno delo

• Preberi še razlago v SDZ 5, str. 71.
• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 4, od str. 73 naprej/1cčd, 3,* 5*, 7*, 11**.

_________________________________________________________________

Modus ali gostiščnica, 1. ura – za učence V. Pirc

SDZ 5, str. 90

torek, 14. 4. 2020

Najprej si oglej spodnji video, ki sem ga pripravil za vas. Po ogledu naredi zapiske, po potrebi lahko še enkrat poslušaš razlago. Nato se loti samostojnega dela.

 

 

Zapiski, ki morajo biti v zvezku.

Modus ali gostiščnica

SDZ 5, str. 90

torek, 14. 4. 2020

Zgled

a) Določimo modus za ocene pri matematiki, ki so: 3,4,3,5,3,3,2.

Reševanje

Najprej uredimo podatke po velikosti.

2,3,3,3,3,4,5

Modus je 3, ker se ta ocena pojavi kar 4-krat (frekvenca podatka).

Odgovor: Modus ali gostiščnica pri matematiki je ocena 3.

Zapomni si

• Frekvenca je število ponovitev posameznega podatka.
• Modus Mo ali gostiščnica je podatek, ki se med danimi podatki največkrat ponovi.
• Določimo ga lahko za številske in opisne podatke.
• Lahko se zgodi, da je več modusov ali pa ga ne moremo določiti.

Samostojno delo

• Preberi še razlago v SDZ 5, str. 90, 91.
• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 5, od str. 92 naprej/1, 2, 3, 5, 6*, 7*.

__________________________________________________________________________________________________________________________

Mediana ali središčnica, 2. ura – za učence V. Pirc

SDZ 5, str. 96

sreda, 15. 4. 2020

Najprej si oglej spodnji video (klikni na povezavo). Uporabi slušalke, govor se prične od 30 sek. naprej. Nato naredi zapiske, glej spodaj. Če česa ne boš razumel, pojdi še enkrat poslušat posnetek. Nato reši naloge iz točke Samostojno delo.

 

 

 

Zapiski, ki morajo biti v zvezku.

Mediana ali središčnica

SDZ 5, str. 96

sreda, 15. 4. 2020

Zgled

Doličimo mediano ali središčnico danim številskim podatkom.

a) 10, 11, 8, 10, 11, 13 in 12

Reševanje

Najprej uredimo podatke po velikosti.

8, 10, 10, 11, 11, 12, 13

Mediana je 11.

b) 1, 2, 4, 3, 7, 8, 10 in 11

Reševanje

Najprej uredimo podatke po velikosti.

1, 2, 2, 4, 7, 8 ,10 in 11

Mediana je (4+7)/2 = 5,5.

Zapomni si

• Podatek, ki leži natanko na sredini vseh po velikosti urejenih podatkov, imenujemo mediana Me ali središčnica.
• Mediano določamo samo številkim podatkom in ne opisnim.
• Mediana je po velikosti srednji podatek, zato ni občutljiva za ekstremne vrednosti med vsemi podatki.

Samostojno delo

• Preberi še razlago v SDZ 5, str. 96, 97.
• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 5, od str. 98 naprej/4, 5, 6, 11*, 12*.

 

 

PREVERJANJE VAŠEGA ZNANJA IN POVRATNA INFORMACIJA UČITELJU – ANKETA – 3. preverjanje znanja

Tukaj je povezava do ankete, ki jo reši do petka, 17. 4. 2020, do 12.00. Rešitve z analizo bodo na spletu isti dan po 14.00.

 

 

 

 

 

 

______________________________________________________________________________________________________________________________

Rešitve 2. preverjanja znanja – ANKETE, z analizo

petek, 10. 4. 2020

Tukaj lahko prenesete naloge.

ANALIZA ANKETE

• Anketo je rešilo 71 od 83 učencev, to je 86 % vseh učencev.
• 59 % učencev je odgovorilo, da snov razume, 36 % delno in 1 % učencev snovi ni razumelo.
• 92 % učencev je rešilo vse naloge.
• Delež rešitev po nalogah:
  • 1. nalogo je pravilno rešilo 83 % vseh učencev.
  • 2. nalogo je pravilno rešilo 62 % vseh učencev.
  • 3. nalogo je pravilno rešilo 84 % vseh učencev.
  • 4. nalogo je pravilno rešilo 83 % vseh učencev.
  • 5. nalogo je pravilno rešilo 55 % vseh učencev.
  • 6. nalogo je pravilno rešilo približno 72 % vseh učencev.
• Odgovori na nekatera vaša vprašanja:
  • Ali je lahko manj nalog?
    • Količina je res minimalna, mogoče bom spremenil kakšno nalogo v dodatno.
  • Zakaj je v anketi nekaj poglavij, ki jih nismo obravnavali?
    • Vsa poglavja ste morali obravnavati. Res pa je, da ste nekatera poglavja obravnavali že dolgo nazaj. Npr. skupina Vike Pirc je valj že obravnavala, ostale skupine ne. Zato teče vzporedni pouk, da se vse skupine poenotijo. Ostale skupine pa so obravnavale npr. aritmetično sredino, zato tega ne razlagam še enkrat za te skupine. Če pa slučajno kdo ni bil takrat prisoten priporočam, da ponovite (obravnavate) vse ure, ki jih tedensko pripravljam.
  • Ali lahko wordove zapiske kopiram v zvezek?
    • Žal ne, potreben je prepis. Pri tem se učite, hkrati pa razvijate tudi grafomotorične spretnosti.
  • Ali so rešitve pravilne?
    • Načeloma bi morale biti.
  • Ali lahko pripravite tudi predavanje?
    • Učne ure v naslednjem tednu bodo pripravljene tudi v glasovno (video obliki). Upam, da vam bo všeč … Bo pa si potrebno razlago poslušati, ker sem zapiske skrčil. Več pa v ponedeljek, ko objavim gradivo za naslednji teden.

2. preverjanje znanja – naloge, valj, aritmetična sredina, verjetnost

1. naloga

Izračunaj površino valja, če meri polmer osnovne ploskve 1,2 dm, višina valja pa je 10 cm (za pi vsemi 3,14, lahko uporabljaš računalo).  

2. naloga

Pri pevskem zboru je 30 učencev, stari so povprečno 15 let. Kaj lahko iz tega sklepamo? 

3. naloga

Igralna kocka ima dve ploskvi rdeči, eno zeleno in tri bele ploskve. Kakšna je verjetnost, da pri metu kocke pade rdeča ploskev? 

4. naloga

Pri košarki je Jure z 20 meti osemkrat zadel koš, Jože pa je v 14 metih koš zadel sedemkrat. Kdo je bil uspešnejši pri metu na koš? 

5. naloga

V trgovini je na polici 13 stogramskih čokolad, 18 čokolad po 250 g in 10 čokolad po 30 dag. Kolikšna je povprečna teža čokolade na polici? 

6. naloga

Osnovna ploskev valja ima ploščino 144π cm2, višina valja je 15 cm.

1. a) obseg osnovne ploskve meri:
2. b) ploščina plašča meri:
3. c) površina valja meri:

Rešitve

 

 

 

 

___________________________________________________________________________________________________________________________

4. TEDEN, 6.4.-10.4.2020

 

Pohvaliti vas moram za reševanje 1. preverjanja znanja. Odlično ste se odrezali, skoraj vsi ste jo rešili pravilno. Anketo vas je kar 85 % vseh učencev, 71 od 83. Bravo, samo tako naprej. Poskusimo doseči 90 %.

Opomba

Pripravljene so tri učne ure. Nekateri učenci ste že obravnavali poglavje Valj, nekateri pa Aritmetično sredino. Vseeno preglejte, če imate ustrezne zapiske in rešene naloge v SDZ  in malo ponovite snov. V zvezku morajo biti obvezno zapiski od dveh ur, ki jih še niste obravnavali. Vseeno pa priporočam, da pregledate tudi poglavje, ki ste ga že obravnavali, v anketi-preverjanju, bodo zajete naloge iz vseh treh učnih enot.

Na koncu poglavij tega tedna je povezava do 2. preverjanja znanja. 

Zapiski, ki jih morate prepisati v zvezek. Poševno besedilo je razlaga, tega ne rabite nujno prepisovati.

              

Ponedeljek, 6. 4. 2020, 1. ura  

Tukaj lahko odprete zapiske tudi v Wordu.                                 

Verjetnost, izražena s števili, SDZ 5, str. 127

Ponovimo

• Zadnjo uro smo spoznali, kaj je to poskus, dogodek, vrste dogodkov in kakšna je verjetnost, da se nek dogodek zgodi.
• Danes bomo spoznali, kako verjetnost izrazimo s števili.

Nova snov

Zgled

• Kolikšna je verjetnost, da pri metu igralne kocke padeta 2 piki?

Reševanje

Poskus je met igralne kocke

Dogodek (za nas ugoden) je, da padeta 2 piki – samo 1 možnost.

Vseh možnosti je 6, lahko pade 1, 2, 3, 4, 5 ali 6 pik.

Število ugodnih dogodkov za nas je, da padeta 2 piki – torej 1 možnost.

Verjetnost, izražena s številom je enaka  1/6. Lahko pa rešitev izrazimo z decimalno številko, 1:6 = 0,166666… Če zaokrožimo na dve decimalki je 0,17 ali izraženo z odstotki to pomeni 0,17 * 100 = 17 % (seveda je to zaokrožen rezultat, točno bi bilo 16,6666666 … %)

• Kolikšna je verjetnost, da iz kupa 52 kart izvlečemo asa?

Reševanje

Poskus je vlečenje igralne karte.

Dogodek (za nas ugoden) je, izvlečena karta je as.

Vseh možnosti je 52.

Število ugodnih dogodkov (možnosti) za nas je, da je izvlečena karta srčev, križev, pikov ali karin as, torej 4 možnosti.

 

Verjetnost, izražena s števili je enaka 4/52 =1/13

Odgovor: Verjetnost, da je izvlečena karta as, je 1/13.

(Rešitev bi lahko izrazili še z odstotki ali decimalno številko. Nikakor pa ne smete zapisati

1 : 13)

 

ZAPOMNI SI

• Verjetnost, izraženo s števili, izračunamo = ŠTEVILO UGODNIH MOŽNOSTI – DOGODKOV/ŠTEVILO VSEH MOŽNOSTI

• Verjetnost pišemo kot ulomek, decimalno število ali odstotek.
• Verjetnost ne pišemo kot razmerje (npr. 1 : 6)
• Verjetnost gotovega dogodka je 1 ali 100 %
• Verjetnost nemogočega dogodka je 0.
• Verjetnost slučajnega dogodka je med več kot 0 in manj kot 1.

Vaja

 

Odpri SDZ 5 na str. 131 preberi in reši 5., 7. a in 9. a nalogo, spodaj preveri rešitve.

Rešitve

 

 

 

Samostojno delo

 

• Preberi še razlago v SDZ 5, str. 127, 128 in 129.
• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 5, od str. 130 naprej/4, 6*, 7, 8, 9, 10*, 11*

 

 

Sreda, 8. 4. 2020, 2. ura

Tukaj lahko odprete zapiske tudi v Wordu.

                                

Aritmetična sredina ali povprečje, SDZ 5, str. 78

Ponovimo

• Zadnjo uro smo spoznali, kako se izračuna verjetnost nekega dogodka. Če se dogodek zagotovo zgodi, je verjetnost 1 ali 100 %, če se ne zgodi, je 0, če je dogodek slučajen, je večja od 0 in manjša od 1. Izračunamo jo tako, da delimo število ugodnih dogodkov z vsemi možnostmi.

Nova snov

• Danes bomo spoznali, kaj je aritmetična sredina, kako jo izračunamo in v katerih primerih jo je smiselno izračunati.

 

Zgled

• Izračunajmo povprečno oceno pri matematiki, če imamo ocene 2, 2, 5, 4, 5, 3 in 4.

Reševanje

Povprečno oceno izračunamo tako, da seštejemo vse podatke in delimo s številom podatkov, torej:  x = (2+3+5+4+5+3+4)/7=24/7=3,43

  

Odg. Povprečna ocena pri matematiki je 3,43.

• Jure je kupil zvezke, 4 po 2,50 € in 2 po 3,40 €. Kolikšna je povprečna cena zvezka?

Reševanje

Povprečno oceno izračunamo tako, da seštejemo vse podatke in delimo s številom podatkov, torej: x = (4*2,50+2*3,40)/6= 16,80/6 = 2,80

      

Odg. Povprečna cena zvezka je 2,80 €.

 

ZAPOMNI SI

• Aritmetično sredino računamo:  VSOTA VSEH PODATKOV/ŠTEVILO PODATKOV

• Aritmetično sredino ali povprečje lahko izračunamo le za številske podatke, za opisne (npr. barva las) je ne moremo izračunati.

• Pri analiziranju podatkov smo previdni, ko računamo aritmetično sredino. Je eden izmed pokazateljev srednjih vrednosti, vendar nas lahko tudi zavede, npr., če en podatek močno odstopa.

Vaja

 

Odpri SDZ 5 na str. 80 preberi in reši 2. in 11. nalogo, spodaj preveri rešitve.

Rešitve 

 

 

 

Samostojno delo

 

• Preberi še razlago v SDZ 5, str. 78-80
• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 5, od str. 80 naprej/1, 4ab, 9, 10, 12*, 13*, 15*, 17*, 18**.

 

 

Sreda, 8. 4. 2020, 2. ura  

Tukaj lahko odprete zapiske tudi v Wordu.                            

Površina valja, SDZ 4, str. 52

Ponovimo

• Zadnjo uro smo spoznali, kako se izračuna verjetnost nekega dogodka. Če se dogodek zagotovo zgodi, je verjetnost 1 ali 100 %, če se ne zgodi, je 0, če je dogodek slučajen, je večja od 0 in manjša od 1. Izračunamo jo tako, da delimo število ugodnih dogodkov z vsemi možnostmi.

Nova snov

• Danes bomo spoznali, kaj je valj, kateri liki so mejne ploskve valja, kako izračunamo površino valja.

Zgled

• Jure želi iz kartona narediti model valja, ki bo 4 cm visok in 3 cm širok. Kakšne ploskve naj izreže?

Reševanje

Valj omejujeta dva enako velika kroga – osnovni ploskvi valja in plašč, ki je v razgrnjeni obliki pravokotnik – spomni se prizme.

Skica

Spomni se, da se ploščina kroga računa πr², obseg kroga pa 2πr, pri čemer je r polmer osnovne ploskve. Plašč je pravokotnik, ploščina je dolžina krat širina. Več v nadaljevanju.

Odg. Jure naj izreže dva skladna kroga s polmerom 1,5 cm ter pravokotnik, dolg 9,4 cm in širok 4 cm.

• Izračunajmo površino valja, če meri polmer r = 12 cm in višina valja v = 8 cm.

Reševanje

Odg. Površina vaja meri 480π cm².

• Izračunaj površino valja, če meri premer 7 cm, višina pa 0,3 dm.

Reševanje

 

Odg. Površina vaja meri 45,5π cm²(točen rezultat) ali 142,87 cm² (rezultat je na dve decimalki natančen).

 

ZAPOMNI SI

• Valj je okroglo telo, ki ga omejujeta dva skladna in vzporedna kroga ter ena kriva ploskev

• Površina valja je enaka vsoti ploščin obeh osnovnih ploskev in plašča

P = 2 O + pl

• Ploščina osnovne ploskve valja (krog) je enaka ploščini kroga

O = πr²

• Ploščina plašča valja, ki je v razgrnjeni obliki pravokotnik

pl = ov=2πrv

• Valj je pokončen, če je dolžina stranice valja enaka njegovi višini

s = v

Vaja

Odpri SDZ 4  na str. 56 preberi in reši 7. nalogo.

Reševanje

 

Samostojno delo

 

• Preberi še razlago v SDZ 4, str. 52, 53
• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 4, od str. 54 naprej/1, 2, 3, 4, 6, 8, 9*, 10*, 13*, 15**.

PREVERJANJE VAŠEGA ZNANJA IN POVRATNA INFORMACIJA UČITELJU – ANKETA – 2. preverjanje znanja

Tukaj je povezava do ankete, ki jo reši do četrtka, 9. aprila. Rešitve bodo na spletu v petek.

 

__________________________________________________________________________________________________________________________

Urednik strani: Franci Kravcar, za vsa vprašanja se obrnite na e-naslov: franci.kravcar@gmail.com, lahko pa jih napišete tukaj. Z veseljem vam bomo pomagali.

 

 

3. teden, od 30. 3. 2020 do 3. 4. 2020

Rešitve 1. preverjanja znanja (1ka).

Prenos v Word –  Rešitve 1. preverjanja znanja

Rešitve 1. preverjanja znanja

Q9 – Katera in koliko dvomestnih števil lahko sestaviš iz števk 4, 5 in 6, če naj se števke v številu ne ponavljajo? Pomagaj si s kombinatoričnim drevesom.

 6 števil
5 števil
4 števila
Kombinatorično drevo:

 

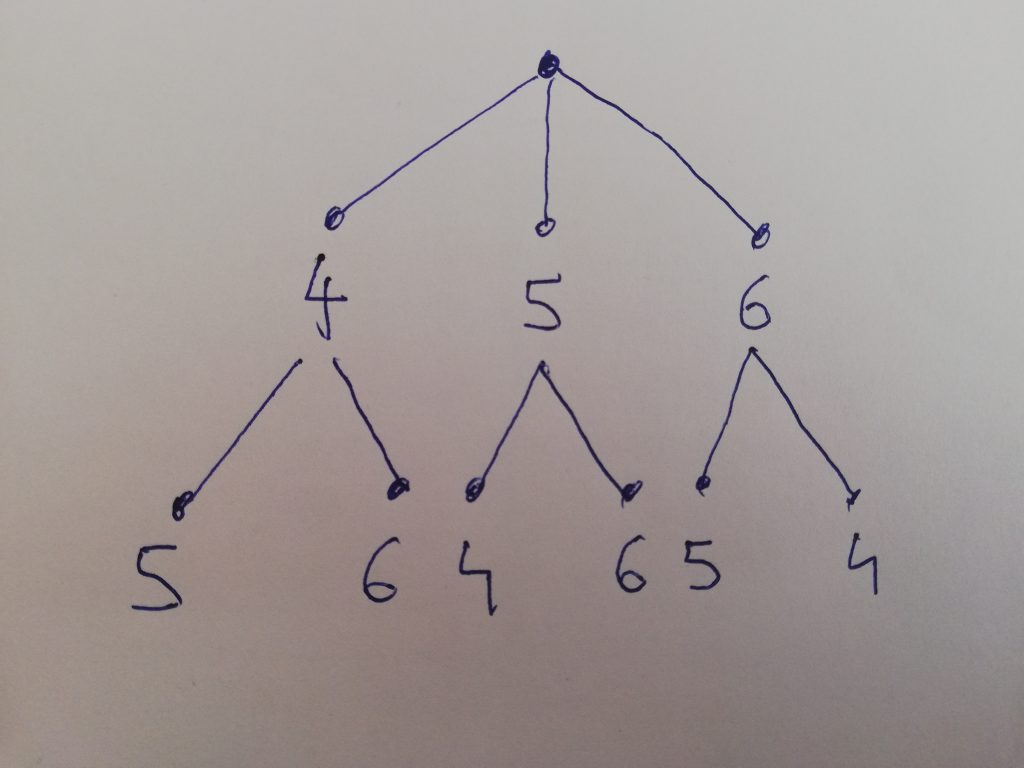
Q10 – Zapiši ta števila.

45, 46, 54, 56, 64, 65

Q11 – Kaj je poskus?

·        Poskus je dejanje, ki ga opravimo po natanko določenih navodilih. Vsak poskus ponuja različno število izidov.

Q12 – Kaj je dogodek?

·        Dogodek je pojav, ki je povezan z izidom poskusa, ki ga proučujemo. Lahko se zgodi ali pa tudi ne.

Q13 – Kaj je frekvenca dogodka?

·        Frekvenca dogodka je število poskusov, pri katerih se je zgodil dani dogodek.

Q14 – Katere tri vrste dogodkov poznaš?

·         Vrste dogodkov: o   Nemogoč dogodek – se nikoli ne zgodi o   Gotov dogodek – se vedno zgodi o   Slučajen dogodek – se lahko zgodi ali pa tudi ne

Q15 – V vreči so zelena, rdeča in dve modri kroglici. Na slepo izvlečemo eno kroglico. Zapiši, za kakšen dogodek gre.

	Nemogoč dogodek.	Gotov dogodek.	Slučajen dogodek.
Izvlečemo rumeno kroglico.	x
Izvlečemo zeleno kroglico.			x
Izvlečemo obarvano kroglico.		x

Ponedeljek, 30. 3. 2020 – 1. ura

Opomba

Nekateri učenci ste že obravnavali poglavje Kombinatorično drevo. Vseeno preglejte, če imate ustrezne zapiske in rešene naloge v SDZ 5 in malo ponovite snov. Nadaljujete z 2. uro, ki bo pripeta naknadno.

Na koncu ne pozabi rešiti anketo.

Zapiski, ki jih morate prepisati v zvezek. Poševno besedilo je razlaga, tega ne rabite nujno prepisovati.

Tukaj lahko odprete zapiske tudi v Wordu.                             

Kombinatorično drevo, SDZ 5, str. 117

Zgled

Trgovec ponuja majice v zeleni, beli in rdeči barvi. Vse majice so velikosti S, M, L in XL.

Koliko različnih majic ima trgovec v ponudbi?

Reševanje

1. Način

(imamo 3 različne barve in 4 velikosti – število majic dobimo, da zmnožimo vse možnosti)

3 * 4 = 12 načinov

 

2. Način – KOMBINATORIČNO DREVO
3. 

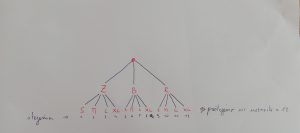
(Vedno naredimo piko – izhodišče, nato prve tri možnosti, iz vsake možnosti pa še število vej za drugo možnost. Na koncu preštejemo vse možnosti, ki so na »zadnji veji«, v pomoč sem spodaj napisal številke.)

Sliko preriši v zvezek.

Odgovor: Trgovec ima 12 različnih majic.

PRAVILA

• Kombinatorično štetje je preštevanje vseh možnih zaporednih izbir.
• Izbira je neodvisna, če nobena naslednja izbira ni odvisna od predhodne.

(dogodki so med seboj neodvisni, saj npr. barva majice ni odvisna od njene velikosti, več se boste naučili v srednji šoli) 

Vaja

Katera in koliko dvomestnih števil lahko sestaviš iz števk 2, 5 in 6, če naj se števke v številu ne ponavljajo? Pomagaj si s kombinatoričnim drevesom.

Reševanje

Sika 1.

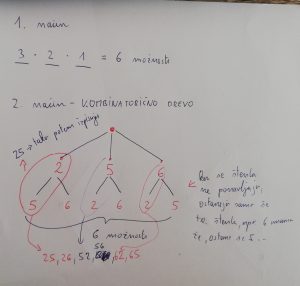
Odgovor: Dobimo 6 števil, to so: 25,26, 52, 56, 62, 65.  

Samostojno delo

• Preberi še razlago v SDZ 5, str. 117 in 118
• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 5, str. 118-120/1, 2, 3, 4*, 6*, 7*.

__________________________________________________________________________________________________________________________

Sreda, 1. 4. 2020 – 2. ura

Zapiski, ki jih morate prepisati v zvezek. Poševno besedilo je razlaga, tega ne rabite nujno prepisovati.

Tukaj lahko odprete zapiske tudi v Wordu.             

       

Poskus. Dogodek. Vrste dogodkov. Verjetnost dogodka, SDZ 5, str. 121

(Danes bomo spoznali, kaj je to poskus, dogodek, vrste dogodkov in kakšna je verjetnost, da se nek dogodek zgodi)

Zgled

Mečemo pošteno igralno kocko. Določi, za katero vrsto dogodka gre:

1. Vržemo 1, 2, 3, 4, 5 ali 6 pik.

Reševanje

Poskus je met igralne kocke

Dogodek je, da pade 1, 2, 3, 4, 5 ali 6 pik.

Če vržemo kocko, zagotovo pade 1, 2, 3, 4, 5 ali 6 pik. Takemu dogodku, ki se zagotovo zgodi, rečemo GOTOV DOGODEK.

1. Vržemo 3 pike.

Reševanje

Poskus je met igralne kocke

Dogodek je, da padejo 3 pike.

Če vržemo kocko, ni nujno, da vedno padejo 3 pike, zato takemu dogodku rečemo  SLUČAJEN (NAKLJUČEN) DOGODEK.

1. Vržemo 8 pike.

Reševanje

Poskus je met igralne kocke

Dogodek je, da pade 8 pik.

Če vržemo kocko, je nemogoče, da pade 8 pik, zato takemu dogodku rečemo  NEMOGOČ DOGODEK.

ZAPOMNI SI

• Poskus je dejanje, ki ga opravimo po natanko določenih navodilih. Vsak poskus ponuja različno število izidov.
• Dogodek je pojav, ki je povezan z izidom poskusa, ki ga proučujemo. Lahko se zgodi ali pa tudi ne.
• Frekvenca dogodka je število poskusov, pri katerih se je zgodil dani dogodek.
• Vrste dogodkov:
  • Nemogoč dogodek – se nikoli ne zgodi
  • Gotov dogodek – se vedno zgodi
  • Slučajen dogodek – se lahko zgodi ali pa tudi ne 

Vaja

Odpri SDZ 5 na str. 125 preberi in reši  9. a nalogo in 12. nalogo.

Reševanje (rešitve)

9. a

Poskus – tekmovanje na plesnem turnirju

Dogodek – Zmaga na plesnem tekmovanju

Dogodek je slučajen (lahko zmagata ali pa tudi ne)

12. naloga

1. a) slučajen dogodek, lahko jo izvlečemo ali pa tudi ne
2. b) nemogoč dogodek, saj zelene kroglice ni v vreči
3. c) gotov dogodek, vsaka kroglica je obarvana

č) slučajen dogodek, izvlečena kroglica je lahko rdeča ali pa tudi ne

  Samostojno delo

• Preberi še razlago v SDZ 5, str. 123 in 124
• Reši naloge in preveri rešitve (naloge z zvezdico so dodatne): SDZ 5, str. 124-126/5, 7, 8, 9, 10, 11*, 13*

PREVERJANJE VAŠEGA ZNANJA IN POVRATNA INFORMACIJA UČITELJU – ANKETA

Tukaj je povezava do ankete, ki jo reši do četrtka, 2. aprila. Rešitve bodo na spletu predvidoma v petek.

________________________________________________________________________________________________________________

2. teden, od 23. 3. 2020 do 27. 3. 2020

 

9. r.

Ponedeljek, 23. 3. 2020

• Rešujete NPZ 2017, zopet predlagam, da si natisnete NPZ in ga rešite, sicer rešujete v zvezek. Zapise v zvezek oziroma pole hranite.

Sreda, 25. 3. 2020

• Rešujete NPZ 2016, zopet predlagam, da si natisnete NPZ in ga rešite, sicer rešujete v zvezek. Zapise v zvezek oziroma pole hranite.

OPOMBA

Povsod morajo biti razvidni postopki reševanje. Obvezno preverite rešitve. Glej pod navodila za vrednotenje.

_________________________________________________________________________________________________________________________

9. r

Navodila za samostojno učenje matematike v 9. r v tednu od 16. do 20. marca 2020.

REŠEVANJE NPZ, 9. r

1. Reši NPZ 2019 in NPZ 2018 – obvezno za vse učence.
   1. NPZ 2006 in NPZ 2007 (dodatna NPZ – priporočena, vendar nista obvezna). Vsebine – naloge, ki so zajete v NPZ, vendar jih v šoli še nismo obravnavali, izpustite.
2. OPOMBA – NPZ natisni in reši. Če nimaš možnosti tiskanja, naloge rešuj v zvezek. Obvezni so postopki! S tem boš dokazoval svoje delo doma, ko se vrneš v šolo. Preveri rešitve (glej pod navodila za vrednotenje).
3. Povezava do NPZ: https://www.ric.si/preverjanje_znanja/predmeti/matematika3/